在计算理论中,摩尔机器有限状态机,其输出值仅由其当前状态确定。 这与Mealy机器形成对比,Mealy机器的输出值由其当前状态和输入值决定。 摩尔机器以爱德华·摩尔(Edward F. Moore)的名字命名,他在1956年的论文“Gedanken-在顺序机器上进行实验”中提出了这一概念。
定义摩尔机器可以定义为6元组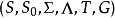 由下列:
由下列:
一组有限的状态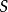 ;
;
起始状态(也称为初始状态)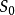 ,它是
,它是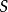 的元素;
的元素;
有限集称为输入字母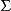 ;
;
有限集称为输出字母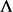 ;
;
转换函数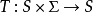 将状态和输入字母映射到下一个状态;
将状态和输入字母映射到下一个状态;
输出函数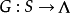 将每个状态映射到输出字母表。
将每个状态映射到输出字母表。
摩尔机器可以被视为限制类型的有限状态换能器。
可视化表示表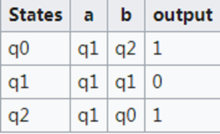
状态转换表是显示输入和状态之间关系的表。
图
Moore机器或Moore图的状态图是将输出值与每个状态相关联的图。 摩尔机器是一个输出生产者。
与Mealy机器的关系由于Moore和Mealy机器都是有限状态机的类型,它们同样具有表现力:任何一种类型都可以用来解析常规语言。
Moore机器和Mealy机器之间的区别在于,在后者中,转换的输出由当前状态和当前输入的组合决定(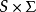 作为
作为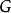 的输入),而不仅仅是当前状态(
的输入),而不仅仅是当前状态(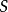 作为
作为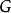 的输入)。当表示为状态图时,
的输入)。当表示为状态图时,
对于Moore机器,每个节点(状态)都标有输出值;
对于Mealy机器,每个弧(过渡)都标有输出值。
每个摩尔机器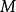 等同于具有相同状态和转换的Mealy机器和输出函数
等同于具有相同状态和转换的Mealy机器和输出函数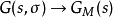 ,它接受每个状态输入对
,它接受每个状态输入对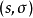 并产生
并产生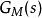 ,其中
,其中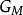 是
是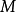 的输出函数。
的输出函数。
但是,并非每台Mealy机器都可以转换为等效的摩尔机器。有些只能转换为几乎等效的摩尔机器,输出时间会发生变化。这是由于状态标签与转换标签配对以形成输入/输出对的方式。考虑从州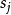 到州
到州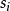 的转换
的转换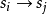 。导致转换的输入
。导致转换的输入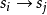 标记边
标记边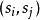 。与该输入对应的输出是状态标签
。与该输入对应的输出是状态标签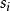 。请注意,这是转换的源状态。因此,对于每个输入,输出在接收输入之前已经固定,并且仅取决于当前状态。这是E. Moore的原始定义。使用状态
。请注意,这是转换的源状态。因此,对于每个输入,输出在接收输入之前已经固定,并且仅取决于当前状态。这是E. Moore的原始定义。使用状态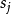 的标签作为转换
的标签作为转换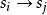 的输出是一个常见的错误。1
的输出是一个常见的错误。1
样例根据输入/输出的数量类型。
简单摩尔机器简单的摩尔机器有一个输入和一个输出:
边缘检测器使用XOR
二进制添加机器
时钟序列系统(限制形式的摩尔机器,其中状态仅在全局时钟信号改变时改变)
大多数数字电子系统设计为时钟顺序系统。时钟顺序系统是Moore机器的受限形式,其中状态仅在全局时钟信号改变时改变。通常,当前状态存储在触发器中,并且全局时钟信号连接到触发器的“时钟”输入。时钟顺序系统是解决亚稳态问题的一种方法。典型的电子摩尔机器包括组合逻辑链,用于将当前状态解码为输出(λ)。当前状态发生变化的瞬间,这些变化会波及该链,并且几乎瞬间输出会更新。有一些设计技术可确保在短暂的时间内输出上不会出现毛刺,而这些变化正在通过链条波动,但大多数系统的设计使得在短暂的转换时间内的毛刺被忽略或无关紧要。然后输出无限期保持不变(LED保持亮,电源保持与电机连接,电磁阀保持通电等),直到Moore机器再次改变状态。
运行实例顺序网络有一个输入和一个输出。 当至少有两个0和两个1作为输入时,输出变为1并且此后保持为1。
图二显示了具有上述描述的九种状态的摩尔机器。 初始状态为状态A,最终状态为状态I.此示例的状态如图三:

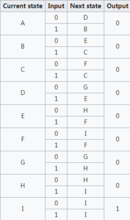
复杂摩尔机器复杂的摩尔机器可以有多个输入和多个输出。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国