最简三角方程(simplest trigonometric equation)亦称基本三角方程,是指含有未知角的基本三角方程,若f(x)是基本三角函数,则f(x)=m(m∈R)称为最简三角方程,凡能用初等方法求解的三角方程,一般都可以通过恒等变换或代数方法归结为解一个或几个这样的最简三角方程,它们的解集的交或并就是原方程的解1。
基本概念设y=S(x)是x的基本三角函数,我们称方程
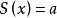 为最简三角方程,即最简三角方程是形如sinx=a,cosx=a,tanx=a,cotx=a,secx=a,cscx=a的几种三角方程,其中a是已知数。
为最简三角方程,即最简三角方程是形如sinx=a,cosx=a,tanx=a,cotx=a,secx=a,cscx=a的几种三角方程,其中a是已知数。
求解最简三角方程求解最简三角方程S(x)=a,就是由函数值a来求出函数S(x)相应自变量的一切值。由于基本三角函数S(x)是周期函数,故可先考虑在一个周期内的对应a的一切x值,再加上周期的整数倍,即得满足S(x)=a的一切x值2。
我们先来讨论最简三角方程
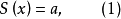
显然,根据正弦函数y=sin x的值域为[-1, 1],故而,当|a|>1时,方程(1)无解。
现在讨论|a|≤1的情况。我们知道,正弦函数y=sin x的周期为2π,故可先在一个周期内求出方程(1)的解。考虑到反正弦函数的值域是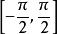 ,故我们选择一个周期
,故我们选择一个周期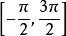 来讨论。
来讨论。
在单位圆中,正弦线等于a的角一般有两个(当a=±1时,看成该两角相重):当a>0时,这两角分别在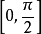 和
和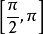 中;当a 1
中;当a 1
∅




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国