[科普中国]-切线三角形

切线三角形(tangent triangle)是一种特殊三角形，指从三角形的各顶点作外接圆切线所成的三角形称为切线三角形。切线三角形是外接圆的极三角形1。

基本概念过△ABC的各个顶点作其外接圆的切线，三切线两两相交于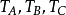 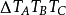， 是△ABC的切线三角形(Tangential Triangle)。它是△ABC外心O的反垂足三角形，也是△ABC的共轭重心的反切瓦三角形，如图1。

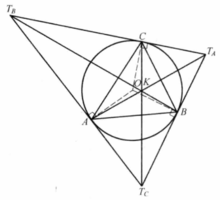
相关性质及定理① △ABC中的共轭重心就是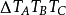 的热尔岗点。

② 切线三角形是外接圆的极三角形。

③ 切线三角形的三线坐标矩阵是

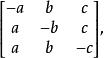其各边的边长是

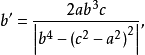
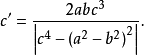其面积是

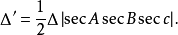
④ 表1中列出了切线三角形内的特征点与原三角形内特征点的对应关系。

|| || 表1

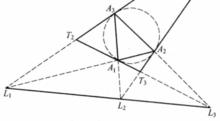
⑤ 给定 和它的切线三角形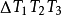 ，两三角形的三条边两两相交于 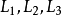，则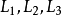 共线，如图22。

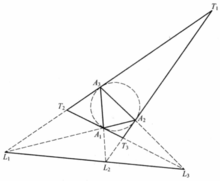
⑥ 切线三角形的外接圆称为切线圆，它的圆心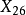是

其半径是

⑦ 下面介绍一个有关切线三角形的定理：

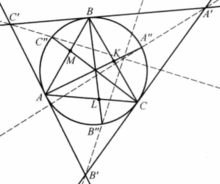
设△ABC的切线三角形是△A'B'C'，设A"，B"，C"是在△ABC外接圆上的任意三点，则有

定理1(斯坦巴特(Stein bart)) 当且仅当直线AA”，BB"和CC"共点，或AA”∩BC，BB"∩CA，CC"∩AB共线时，A'A"，B'B"和C'C"共点，如图32。

本词条内容贡献者为:

李岳阳 - 副教授 - 江南大学