[科普中国]-AKS素数测试

AKS素数测试（又被称为 Agrawal–Kayal–Saxena素数测试 和 Cyclotomic AKS test）是一个决定型素数测试算法 ，由三个来自印度坎普尔理工学院的计算机科学家，Manindra Agrawal、Neeraj Kayal和Nitin Saxena，在2002年8月6日发表于一篇题为素数属于P的论文。1作者们因此获得了许多奖项，包含了2006年的哥德尔奖和2006年的Fulkerson Prize。这个算法可以在多项式时间之内，决定一个给定整数是素数或者合数。

重要性AKS最关键的重要性在于它是第一个被发表的一般的、多项式的、确定性的和无仰赖的素数判定算法。先前的算法至多达到了其中三点，但从未达到全部四个。

AKS算法可以被用于检测任何一般的给定数字是否为素数。很多已知的高速判定算法只适用于满足特定条件的素数。例如，卢卡斯-莱默检验法仅对梅森素数适用，而Pépin测试仅对费马数适用。

算法的最长运行时间可以被表为一个目标数字长度的多项式。ECPP和APR能够判断一个给定数字是否为素数，但无法对所有输入给出多项式时间范围。

算法可以确定性地判断一个给定数字是否为素数。随机测试算法，例如米勒-拉宾检验和Baillie–PSW，可以在多项式时间内对给定数字进行校验，但只能给出概率性的结果。

AKS算法并未“仰赖”任何未证明猜想。一个反例是确定性米勒检验：该算法可以在多项式时间内对所有输入给出确定性结果，但其正确性却基于尚未被证明的广义黎曼猜想。

概念AKS 素数测试主要是基于以下定理：整数n(≥ 2)是素数，当且仅当1

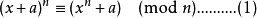这个同余多项式对所有与n互素的整数a均成立。 这个定理是费马小定理的一般化，并且可以简单的使用二项式定理跟二项式系数的这个特征:

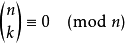，对任何 00 且b>1 ，令n=a；则输出合数；

找出最小的r令ordr(n)>log(n)；

若 对某些a≤r，1