[科普中国]-那塞特热传系数

又称“那塞特准则”，是对流换热研究中借以确定对流换热系数的待定准则数，为一无量纲综合量，常用符号Nu表示。其值常通过实验或由求解相关的准则方程式而得到。Nu与无量纲温度分布在壁面上的梯度有关,可以反映流体的导热热阻与其对流换热热阻的比值。因此在其他条件均相同的情况下,那塞特热传系数愈大表明发生于流体与固体壁面之间的对流换热过愈为强烈。1

概念详解对流换热传递能量时,要受传导及物质传递两方面的影响。除了液体金属以外,一般流体的导热系数都比较小,所以能量的传递主要依靠流体粒子的混乱运动。

如果流速及紊流的强度都较小,那那么宏观的混合运动也弱,对能量的传递大为不利。当流速增加时,能促进低温流体与高温流体间的混合运动,这虽对单纯的传导机理不重要,但是,对能量传递却很有利。因此,通过热对流要传递某一定量的热量时,低速区域要比高速区域需要较大的温度梯度。

如果采用这些定性考察的结果,那么,可以粗略地描述由固体壁向形成素流的流体传热过程中产生的流体温度分布。在贴近壁面处,由于流体粒子相对于边界是静止的,这时热仅通过热传导传递。因此,这一层会产生较大的温度梯度。再远离壁面时,由于流体的混合运动有利于能量的传递,所以,此处的温度梯度较缓和,在主流内则没有温度梯度。

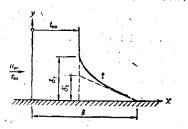如右图所表示的那样。通常,把从壁面开始到无温度梯度点的距离 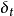称为温度边界层的厚度( thermal-beunday layer),在此外侧的流体温度等于主流的温度 。

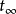如上所述，在界面处（y=0）因热量只由传导传递,所以由壁面向流体的传热量可由下式表示：

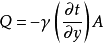
在已知温度分布的情况下，可以利用这个传热量计算公式进行计算，但在工业上计算传热时用传热系数比较便利,所以为了不失掉其物理上的含义，有必要引进传热系数与界面处流体温度梯度的关系。

下面取流体的代表温度为主流温度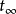 时,来定义传热系数α,由对流换热定律及壁面向流体的传热量计算公式联立得：

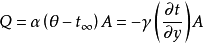
引入指定换热面系统形状的特征尺l，将上式改写成无量纲形式,则可得

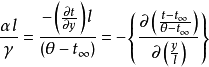
式中左边由传热系数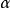,特征尺寸l及导热系数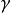组成的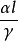是无量纲数,并将此定名为那塞特热传系数,用符号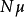表示。在物理意义上它表示了壁面处流体温度梯度与标准温度梯度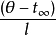之比，是一个含有对流传热系数的无量纲特征数。

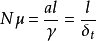
由上式可知，如果等效热传导层厚度变小，则对流热阻也变小，为了迅速传递更多的热量,就必须把温度边界层的厚度尽量弄薄。为此，只要增加流速及使流动变成紊流状态就可以了。若以表面隔热为目的，则制造厚而静止的边界层是有利的。事实上，只要不引起混合运动，则有小空隙的隔热材料由于空气导热系数小,对隔热有利。2

本词条内容贡献者为:

李航 - 副教授 - 西南大学