[科普中国]-规形定理

规形定理(theorem of compasses form)是在完全四边形边上求分点比值的定理。在折线BAC的BA，AC两线段上各取一点D、E，设CD，BE交于点F，若BD=DA=1∶λ，CE∶EA=1∶μ，则必BF∶FE= 1∶(λ/(1+μ))，CF∶FD= 1∶(μ/(1+λ)) 1。

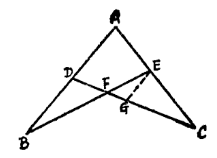
定理介绍规形定理 如图1，完全四边形ADFEBC中，在折线BAC的BA，AC两线段上各取一点D、E，设CD，BE交于点F，若BD=DA=1∶λ，CE∶EA=1∶μ，则必

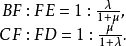
应用此定理对形如二脚规的凹四边形在已知部分分点所得比值的情况下，可求出另外分点的比值2。

规形定理的证明证明 如图1，过E引EG//AB，且交DC于G、注意△EGF∽△BDF及△CEG∽△CAD，有

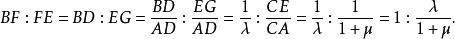
同理可证另一式1。

规形定理的说明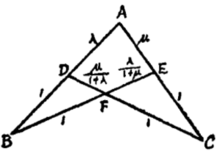

说明：

(1) 规形定理可以用图2表示。我们在BD边上标出1，DA边上标出λ……，不表示BD长为1，DA长为λ，只表示在同一直线上的两线段的比例数，即指BD:DA=1:λ。

(2) 由于图2外形像一只二脚规，故称文中定理为“规形定理”，规形外壳为一凹四边形，可称图2为规形FCAB。

(3) 必须熟记图2中各线段的比例数，其中特别注意从“足尖" B、C出发的四条线段的比例数均定为11。

规形定理的应用下面举例来说明” 规形定理”的应用1。

【例1】在△ABC的BC和CA边上分别取P，Q，使BP:PC=1:2，CQ:QA=2:3，连AP，BQ交于R，求AR:RP是多少?

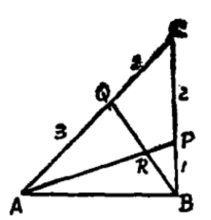
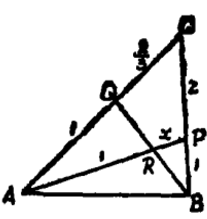
解：依题意作出图3，与图2对照，把各比例数标准化得图4，此处的标准化，是指从“足尖”出发的各线段的比例数均要定为1 (注意:当AQ的比例数定为1时，QC的比例数就为2/3)，令AR:RP=1:x，则依规形定理，有:

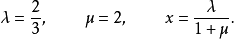故得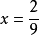，从而AR:RP=1:x=9:2。

【例2】在△ABC中， D在AB上，且使AD:DB=1:2，而G在CD上，且使CG:GD=3:2，如果BG交AC于F，求BG:GF?

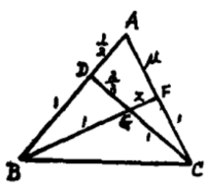
解：依题意作出图5，其中规形GBAC的各比例数已标准化，即得：

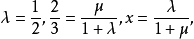逐得:

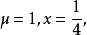故

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学