[科普中国]-铰链四边形

铰链四边形(hinge quadrilateral)是一种特殊的四边形，如果四边形的四条边的边长一定，其四个内角不固定，这样的可以变形的四边形称为铰链四边形，铰链四边形显示四边形的不稳定性。

基本概念如果四边形的四条边的边长一定，其四个内角不固定，这样的四边形就叫做铰链四边形，铰链四边形的任三边长度之和大于第四边，铰链四边形还有一个重要的性质：在四边长度给定的一切四边形中，内接于圆的四边形具有最大的面积。

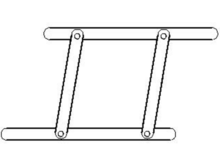
相关定理我们知道，一个三角形在三边长度给定的条件下，这个三角形的形状及它的面积就被惟一地确定下来，但对四边形来讲，情况就大不相同了，当四边长度给定时，可以做出各种各样形状的四边形。譬如，我们取长度分别为a、b、c、d的四根小木条，并用铰链联成一个活动的四边形(图2)，活动这个四边形的顶角。便可得到各种形状的四边形，这些四边形具有不同的面积。那么在这些四边形中，怎么样的四边形具有最大的面积?

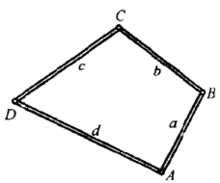
下面的定理回答了这个问题（关于定理的证明请参考相应书籍1）。

定理1 在四边长度给定的一切四边形中，内接于圆的四边形具有最大的面积。

细心的读者可能会提出这样的问题：难道在边长给定的条件下，适当调整夹角一定能使四边形内接于圆吗?

引理 在保持四边形各边长度的条件下，适当调整它的顶角，一定能够使它内接于圆1。

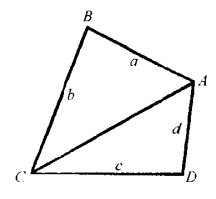
铰链四边形的面积当四边长度给定时，四边形面积的最大值

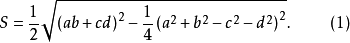这也就是四边给定且又内接于圆的一般四边形的面积公式1。

设a+b+c+d=2p，公式(1)能改写成更对称更完整且便于记忆的形式

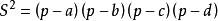或

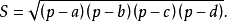
这个关于a、b、c、d具有对称形式的公式还告诉我们:面枳的最大值与给定边的次序无关，仅由给定的边长a、b、c、d惟一确定。

假如四辺形ABCD的边长中有一边的长度逐渐缩短而最后趋于零，譬如DA=d=0，此吋，四边形退化为三角形，任何三角形都内接于圆，故得三角形面积

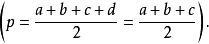这就是著名的海伦公式。因此，上述公式是海伦公式的推广。

公式(1)：

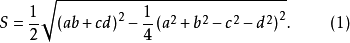是我国南宋数学家秦九韶在他所著《数书九章》中的三斜求积(已知三边求三角形的面积)公

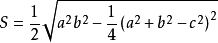的推广1。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所