[科普中国]-多焦点曲线

到n个定点的距离之和为定值（半径的平方）的点的轨迹，称为n焦点曲线（多焦点曲线），圆、椭圆、卵圆，都是多焦点曲线1。

定义到 个定点的距离之和为定值的点的轨迹，称为 焦点曲线2。

平面上，给定 个定点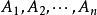 ，其坐标分别是 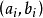，自由点。

由以下方程所确定的曲线Ω，就是 焦点曲线，前提是 存在。

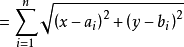
具体内容当 时，Ω 是圆；

当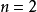 时，Ω 代表椭圆；

当 时，情况就复杂了，因为方程不可能化成有理式。

当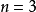 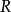， 最小时，Ω退化成一个点，正是 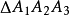的费尔马点。当然有可能 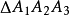退化成直线型或者某两个点重合。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学