[科普中国]-夏普尔定理

夏普尔定理(Chapple theorem)亦称欧拉定理，是关于三角形外接圆和内切圆半径与圆心距的关系定理，若△ABC的外接圆半径为R，内切圆(或旁切圆)半径为r，内切圆与外接圆的圆心距为d，则d²=R²±2Rr，等式中对于内切圆取负号，对于旁切圆取正号1。

定理及简史设⊙O₁、⊙O₂的半径分别为r和R，圆心距为d，若存在一个三角形以⊙O₁为内切圆(或旁切圆)，同时又内接于圆⊙O₂，则

或

当⊙O₁为内切圆时取“-”号，为旁切圆时取“+”号。

上述定理被称夏普尔定理(Chapple theorem)或称为关于三角形的欧拉定理，但不论属于谁，这一定理的发现至今已有二百多年的历史，而且欧拉的学生富斯(N.Fuss,1755 ~ 1825)在1798年还给出了它的一个推广2。

定理的证明证明 如图1(a)，联结AO₁，设其所在直线交⊙O₂于D，联结BD，再过O₁作⊙O₂的直径EF，则由圆幂定理有

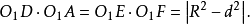又

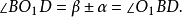(内切时取“+”号,旁切时取“一”号)，所以

从而有

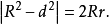当⊙O₁为内切圆时，R>d，有d²=R²-2Rr；当⊙O₁为旁切圆时，R