[科普中国]-游移切线法作图

在几何作图中，当所作图形的某边(角)需与一已知的弦等长(或已知内接角相等)，并又需满足其它条件时：可以先作出已知弦长的轨迹圆；然后从另一条件出发，在适当的位置向轨迹圆作出切线，来实现作图的要求。这种作图方法，称为游移切线法。

基本介绍游移切线法作图(constructing by shifting tangent)是作图方法的一种，如果作图的关键在于确定某一直线的位置，可暂时放弃这直线所应满足的条件之一，于是这直线可能因位置不定而常切于某曲线，而这曲线实际就是点的轨迹(例如圆)，这样一来，只要先把这轨迹作出，然后作它的某切线，使它符合所放弃的条件，问题便得以解决，用这种方法作图称为游移切线法作图，一般都是圆或圆弧，而不适宜用于别的曲线。

例如，在已知直线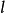 上求一点M1，使它向已知圆⊙O(r)所引切线长等于已知长a(如图1)。

设M1是已知直线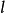 上符合条件的点，M1D1为从点M1向已知圆所引的切线，OD1=r，M1D1=a。问题关键在确定点M1在直线 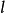上的位置，若暂不考虑点M1须在直线 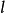上的条件，只研究点M到圆O所引切线MD须等于已知长a，它便是⊙O(r)的一条游移切线，端点M到⊙O(r)圆心O的距离

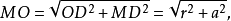其轨迹是已知圆的一个同心圆C，它与直线 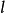的公共点便是所求的点，因此，M1便是圆C与直线 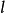的公共点。

当圆C与直线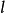 相切时，一解；当圆C与直线 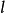相交时，二解；当圆C与直线 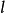相离时，无解1。

例题解析例1以一固定线段为一边求作平行四边形，使已知边的对边恰好是一定圆的弦。

已知：一定圆O，一固定线段AB。

求作：平行四边形ABCD，使AB为固定线段，对边CD为圆O的一弦。

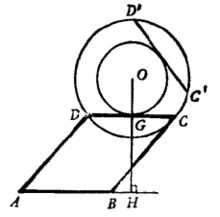
分析: 设图已成 (图2)。 因平行四边形的对边平行且相等、 可知AB//CD，CD= AB；又因线段AB固定，故可先作出弦长等于AB的轨迹圆，再作平行于AB的轨迹圆切线，即可确定C、D、二点。

作法：

(1) 在圆O上作弦C'D= AB；作弦长等于C'D'的轨迹圆O(C'D')。

(2) 作OH⊥AB，交圆O(C'D') 于G；过G作AB的平行线，交圆O于C、D二点。

(3)连BC、 AD，平行四边形ABCD作成。

证明：据作图OH⊥AB, CD// AB，知OG⊥CD，则CD为圆O(C'D')的切线，故CD=C'D'= AB。 可见，线段AB与弦CD平行且相等，故知ABCD必为平行四边形。

讨论：设圆O直径为d，其解数有以下三种情况：

(1) 当ABd时，无解2。

例2 求过定点作定圆的内接三角形，使内接三角形的一边所在直线过定点，内接三角形的边长比为已知线段比。

已知: 一定圆O、一定点P及三已知线段a、b、c。

求作:内接三角形ABC，使一边所在直线过P点，且BC:AC:AB = a:b:c (图3)

分析:设图已成。

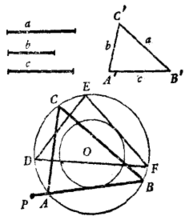
(1)因三角形的边长比一定，其三个角必为一定。因此可用已知线段a、b、c作出内接三角形的相似三角形△A'B'C'，定其三个角， 以便作图。

(2) 内接三角形在确定三个角以后，如何通过P点来作图呢?这需借助于游移切线法。可作圆O内接三角形△DEF，使∠D等于一已知角；再作圆O的一同心圆O(EF)，使与∠D的对边

弦EF相切。可知，在圆O内与圆O(EF)相切之弦，必与弦EF相等，其对应的内接角必等于∠D。因此， 过P点作圆O(EF)的切线，在圆O上可得一已知内接角的弓形弧，然后再以切线弦AB为一角边作圆周角∠B，使等于另一已知角，该角与圆O得交点C，连AC，△ABC即作出。

作法:

(1)以a、b、为三边，作△A'B'C'。

(2)作圆O内接△DEF，使∠D= ∠C'。

(3)作弦EF的轨迹圆O(小)。

(4)过P点作圆O (小)的切线， 交圆O于A、B。

(5)作∠CBA=∠B'，交圆O于C。

(6)连AC，∠ABC即为求作的内接三角形。

证明：因弦AB和弦EF同与圆O (小)相切，知弦，AB= EF, 则∠C=∠D=∠C'；据作图∠B=∠B’，故知△ABC∽△A'B'C'，则知BC:AC:AB= B'C':A'C':A'B'=a:b:c。△ABC符合作图要求。

讨论:本题因P点落在内接三角形的哪一个边上，并没有规定，且P点在内接三角形一边上的位置又有所不同，故解数可以较多。为了便于讨论，设△ABC (或△A'B'C'的一相似内接三角形)三边的弦心距分别为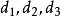 。其解数情况如下:

(1)不符合条件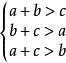 时，无解；

(2)符合上述条件时，

①当d1>OP、d2>OP、d3>OP，无解;

②当d1>OP、d2>OP、d3=OP，有一解，

③当d1>OP、d2>OP、d3OP、d2=OP、d3OP、d2