[科普中国]-奥倍尔定理

奥倍尔定理(Auber theorem)是关于共线点的一个定理，通过△ABC的三顶点引互相平行的三条直线，它们和△ABC外接圆的交点分别为A′，B′，C′，若在△ABC外接圆上取一点P，设PA′，PB′，PC′与△ABC的三边BC，CA，AB或其延长线的交点分别为D，E，F，则D，E，F三点在同一条直线上1。

基本介绍通过△ABC的项点A、B、C引互相平行的三条直线，设它们和△ABC的外接圆的交点分别为A’、B'、C'，在△ABC的外接圆周上取一点P，设PA'、PB'、PC'与△ABC的三边BC、CA、AC或其延长线的交点分别为D、E、F，则D、E、F三点在同一直线上(图1)2。

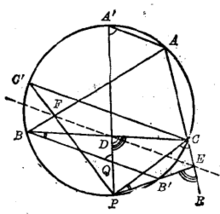
定理的证明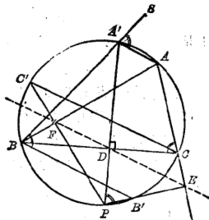

首先请注意，因为A、A'、P、C四点在同一圆周上，所以

∠PCE=∠AA'P， (1)

其次，因为AA'//BB'，如果设PA'和BB'的交点为Q，则有

∠AA'P= ∠BQD.

从这两个式子，有

∠PCE=∠ BQD.

另一方面，因为∠CPE和∠CBB'是同一弦CB'所对的圆周角，所以

∠CPE=∠CBB'.

将这两式相加，

∠PCE+∠CPE=∠BQD + /CBB'，

即如把CE的延长线记作CER，则

∠PER=∠PDC.

这说明P、D、C、E四点在同一圆周上，由此，

∠PCE=∠ PDE. (2)

从(1)、(2)两式，有

∠AA'P=∠PDE.

这表示AA' // DE。完全同样地，可以证明AA' //DF，据此，D、E、F三点在同一直线上。

另外，在奥倍尔定理中，假设有PA'⊥BC 成立(图2)。这时，如设BA'的延长线为BA'S，因为AA'// BB'，所以

∠SA'A=∠A'BB'.

但是因为A'、B、C、A四点在同一圆周上，所以

∠SA'A=∠ACB.

又因为∠A'BB'和∠A'PB'是同一弦A'B'所对的圆周角，所以

∠A'BB'=∠A'PB'，

于是

∠ACB=∠A'PB'.

这个式子表示P、D、C、E四点在同一圆周上。但因为∠PDC=∠R，所以∠PEC=∠R。

同理可证∠PFB=∠R。

于是，在PA'⊥BC的情形，奥倍尔定理成为西摩松定理2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所