[科普中国]-戴维士定理

戴维士定理(Davis theorem)是关于六点共圆的一个重要定理。三角形的每边所在直线上有一对点(可以重合)，若每两对点同在一圆上，则三对点(六点)都在同一圆上(题设中的圆与该线切于重合的点，则为重合的对点)1。

基本介绍定理若三角形的各边或其延长线上各有一对点，其中每两对点为共圆点，则六点为共圆点。如图，在△ABC中，D，E；F，G；H，K分别为三边或其延长线上的一对点，若D，E，F，G；F，G，H，K；H，K，D，E分别共圆，则六点D，E，F，G，H，K为共圆点2。

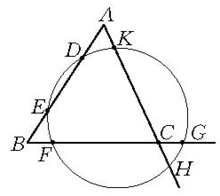
证明若所说三圆不重合 ，则根据根轴的性质(共点或平行).三角形的三条边就得共点或互相平行，但这明明不可能，所以三圆非合一不可2。

具体应用下面给出如上定理的应用例子，

【例1】自直角三角形斜边上高线中点作三边的平行线，与三边相交得到的六个交点共圆2。

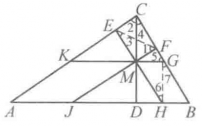
证明 如图2，设M为Rt△ABC的斜边AB上的高线CD的中点，过点M分别与AB，BC，CA平行的线交这三边于J，H，G，F，E，K。

联结EF，GH，由C，E，M，F四点共圆知∠1 =∠2=∠B，∠3=∠4=∠A，

则∠5+∠KEF=∠B+(90°+∠3)=∠B+90°+∠A=180°。

这说明K，E，F，G四点共圆。

又注意到J是AD的中点，G，H分别是BC，DB的中点，那么GH //CD，于是∠7 =∠4=∠A=∠FJ H，从而J，H，G，F四点共圆。

同理，E，K，J，H四点共圆。

故由戴维士定理，知J，H，G，F，E，K六点共圆。

注：也可先证K、E、F、G四点共圆，再证E、F、G、H四点共圆(∠7=∠3)最后证J、K、E、F四点共圆，而证得六点共圆。

【例2】 已知H是锐角△ABC的垂心，以边BC的中点为圆心，过点H的圆与直线BC相交于A₁，A₂两点；以边CA的中点为圆心，过点H的圆与直线CA相交于B₁，B₂两点；以边AB的中点为圆心，过点H的圆与直线AB相交于C₁，C₂两点，证明：A₁，A₂，B₁，B₂，C₁，C₂六点共圆。

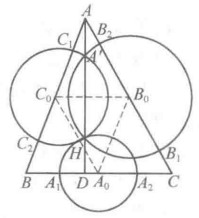
证明 如图3，设B0，C0分别为边CA、AB的中点，又设以B0为圆心过点H的圆与以C0为圆心且过点H的圆的另一个交点为A'，则A'H⊥C0B0。

又C0B0// BC，则A'H⊥BC，于是知点A'在AH上。

由切割线定理，得AC₁：AC₂=AA'·AH=AB₁·AB₂，知

B₁，B₂，C₁，C₂四点共圆。

同理，A₁，A₂，C₁，C₂及A₁，A₂，B₁，B₂分别四点共圆。

故由戴维士定理，知A₁，A₂，B₁，B₂，C₁，C₂六点共圆2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学