[科普中国]-判别损失

判别损失又称“分辨法”，是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

其基本原理是按照一定的判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标。据此即可确定某一样本属于何类。

当得到一个新的样品数据，要确定该样品属于已知类型中哪一类，这类问题属于判别分析问题。

概念判别损失技术是由费舍(R．A．Fisher)于1936年提出的。它是根据观察或测量到的若干变量值判断研究对象如何分类的方法。具体地讲，就是已知一定数量案例的一个分组变量和这些案例的一些特征变量，确定分组变量和特征变量之间的数量关系，建立判别函数，然后便可以利用这一数量关系对其他已知特征变量信息，但未知分组类型所属的案例进行判别分组。

判别损失技术曾经在许多领域得到成功的应用，例如医学实践中根据各种化验结果、疾病症状、体征判断患者患的是什么疾病；体育选材中根据运动员的体形、运动成绩、生理指标、心理素质指标、遗传因素判断是否选人运动队继续培养；还有动物、植物分类，儿童心理测验，地理区划的经济差异，决策行为预测等。1

基本条件判别损失的基本条件是：分组变量的水平必须大于或等于2，每组案例的规模必须至少在一个以上；各判别变量的测度水平必须在间距测度等级以上，即各判别变量的数据必须为等距或等比数据；各分组的案例在各判别变量的数值上能够体现差别。判别损失对判别变量有三个基本假设。其一是每一个判别变量不能是其他判别变量的线性组合。否则将无法估计判别函数，或者虽然能够求解但参数估计的标准误差很大，以致于参数估计统计性不显著。其二是各组案例的协方差矩阵相等。在此条件下，可以使用很简单的公式来计算判别函数和进行显著性检验。其三是各判别变量之间具有多元正态分布，即每个变量对于所有其他变量的固定值有正态分布。

沿用多元回归模型的称谓，在判别损失中称分组变量为因变量，而用以分组的其他特征变量称为判别变量(Discriminant Variable)或自变量。

判别损失的基本模型就是判别函数，它表示为分组变量与满足假设的条件的判别变量的线性函数关系，其数学形式为：

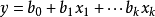
其中，y是判别函数值，又简称为判别值(Discriminant Score)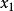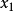；为各判别变量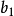；为相应的判别系数(Discriminant Coefficient or Weight)，表示各判别变量对于判别函数值的影响，其中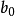是常数项。

判别模型对应的几何解释是，各判别变量代表了k维空间，每个案例按其判别变量值称为这k维空间中的一个点。如果各组案例就其判别变量值有明显不同，就意味着每一组将会在这一空间的某一部分形成明显分离的蜂集点群。我们可以计算此领域的中心以概括这个组的位置。中心的位置可以用这个组别中各案例在每个变量上的组平均值作为其坐标值。因为每个中心代表了所在组的基本位置，我们可以通过研究它们来取得对于这些分组之间差别的理解。这个线性函数应该能够在把P维空间中的所有点转化为一维数值之后，既能最大限度地缩小同类中各个样本点之间的差异，又能最大限度地扩大不同类别中各个样本点之间的差异，这样才可能获得较高的判别效率。在这里借用了一元方差分析的思想，即依据组问均方差与组内均方差之比最大的原则来进行判别。1

基本思想根据判别中的组数，可以分为两组判别损失和多组判别损失；

根据判别函数的形式，可以分为线性判别和非线性判别；

根据判别式处理变量的方法不同，可以分为逐步判别、序贯判别等；

根据判别标准不同，可以分为距离判别、Fisher判别、Bayes判别法等。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所