布罗卡尔三角形(Brocard triangle)是一些特殊点构成的三角形:1.设S为△ABC的外心,K为它的陪位重心,以SK为直径作圆,称这个圆为△ABC的布罗卡尔圆,该圆交三边的勒穆瓦纳平行线于A′,B′,C′,则△A′B′C′称为第一布罗卡尔三角形。2.若K为△ABC的陪位重心,连结AK,BK,CK,与△ABC的布罗卡尔圆分别交于A″,B″,C″,则△A″B″C″称为第二布罗卡尔三角形1。
基本概念如图1,从△ABC的外心O0至类似重心K,以OK为直径作圆,称为布罗卡尔圆。
从O垂直于原三角形的各边,作三线,交布罗卡尔圆于A',B',C',那么△A'B'C'称为第一布罗卡尔三角形。
从△ABC的各角顶至K,作三线,交布罗卡尔圆于A",B",C",那么△A"B"C"称为第二布罗卡尔三角形。
从△ABC的各角顶,平行于△A'B'C'的各边,作三线,共交于一点S,该点称为施泰纳点。

相关证明【例1】三角形的第一布罗卡尔三角形以布罗卡尔圆为外接圆2。

分析 设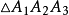 中O为外心,K为类似重点,
中O为外心,K为类似重点,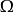 为正Brocard点,
为正Brocard点,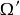 为负Brocard点,
为负Brocard点,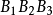 为第一Brocard三角形,如图2,为证B1在以OK为直径的圆上,只须证明∠OB₁K=90°。
为第一Brocard三角形,如图2,为证B1在以OK为直径的圆上,只须证明∠OB₁K=90°。
注意到△B₁A2A3是等腰三角形,底角等于ω,故B₁在A2A3的垂直平分线O1O上,而且B1O1= 。
。
因此,欲证OB₁⊥B₁K,只须证明B₁K//A2A3,为此,可证明K到A2A3的距离KK1=B1O1= 。
。
KK₁= KQ₃sinA₁,KQ₃:R=tgω,式中R表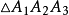 的外接圆半径,故
的外接圆半径,故
 故B₁在OK为直径的圆上。同理可证B₂,B₃亦在此圆上,即第一Brocard三角形
故B₁在OK为直径的圆上。同理可证B₂,B₃亦在此圆上,即第一Brocard三角形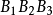 内接于Brocard圆。
内接于Brocard圆。
【例2】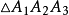 与其第一布罗卡尔三角形
与其第一布罗卡尔三角形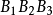 有透视关系,即A₁B₁,A₂B₂,A₃B₃共点D。
有透视关系,即A₁B₁,A₂B₂,A₃B₃共点D。
证: 如图2,A₁B₃,A₂B₁,A₃B₂共点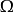 ,A₁B₂,A₂B₃,A₃B₁共点
,A₁B₂,A₂B₃,A₃B₁共点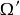 ,即
,即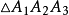 与
与 有透视关系,又与
有透视关系,又与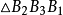 有透视关系,
有透视关系,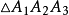 与
与 亦有透视关系,即A₁B₁,A₂B₂,A₃B₃交于一点D。
亦有透视关系,即A₁B₁,A₂B₂,A₃B₃交于一点D。
设过A₁,A₂而且切A₃A₁于A₁的圆,与过A₁,A₃而且切A₁A₂于A₁的圆交于点C₁,过A₂, A₃而且切A₁A₂于A₂的圆,与过A₂A₁而且切A₂A₃于A₂的圆交于点C₂,过A₃,A₁而且切A₂ A₃于A₃的圆与过A₃, A₂而且切A₃A₁于A₃的圆交于点C₃,则△C₁C₂C₃叫做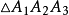 的第二Brocard三角形2。
的第二Brocard三角形2。
本词条内容贡献者为:
尹维龙 - 副教授 - 哈尔滨工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国