施泰纳定理(Steiner theorem),也称为平行轴定理,通过物体的重心和轴线之间的垂直距离在平行轴上的转动惯量,可用于确定给定刚体的质量惯性矩或面积的二次矩。
质量惯性矩假设质量体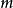 围绕穿过身体重心轴
围绕穿过身体重心轴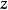 旋转,主体相对于该轴具有
旋转,主体相对于该轴具有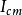 的惯性矩。施泰纳定理指出,如果主体围绕与第一轴平行并且偏离距离
的惯性矩。施泰纳定理指出,如果主体围绕与第一轴平行并且偏离距离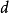 的新轴
的新轴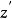 旋转,则惯性矩
旋转,则惯性矩 相对于新轴是与
相对于新轴是与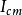 通过下式相关:
通过下式相关:
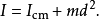 显然,
显然,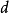 是轴
是轴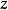 和
和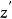 之间的垂直距离。如图1所示,围绕轴的质量体的惯性矩可以由围绕穿过质心的平行轴的质量惯性矩确定。
之间的垂直距离。如图1所示,围绕轴的质量体的惯性矩可以由围绕穿过质心的平行轴的质量惯性矩确定。
施泰纳定理可以应用拉伸规则和垂直轴定理来找到各种形状的惯性矩。
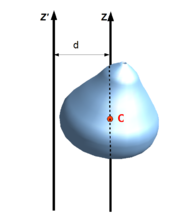
推导在一般性的情况下,假设在笛卡尔坐标系中,轴之间的距离垂直于 轴,并且质心位于原点。相对于
轴,并且质心位于原点。相对于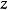 轴的惯性矩是
轴的惯性矩是
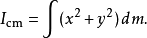 相对于轴
相对于轴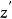 的惯性矩是沿着
的惯性矩是沿着 轴与质心的垂直距离
轴与质心的垂直距离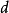 ,
,
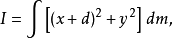
括号内扩展产生
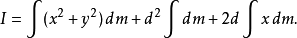 第一项是
第一项是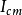 ;第二项是
;第二项是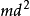 ;最后一项的积分是质心
;最后一项的积分是质心 坐标的倍数,由于质心位于原点,因此为零。因此,等式变为:
坐标的倍数,由于质心位于原点,因此为零。因此,等式变为:
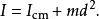
面积惯性矩施泰纳定理也适用于平面区域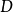 的面积的第二矩(面积惯性矩):
的面积的第二矩(面积惯性矩):
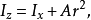 其中
其中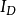 是
是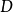 相对于平行轴的面积惯性矩,
相对于平行轴的面积惯性矩,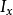 是
是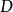 相对于其质心的面积惯性矩,
相对于其质心的面积惯性矩,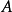 是平面区域
是平面区域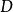 的面积,
的面积, 是距离新的距离轴
是距离新的距离轴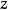 到平面区域
到平面区域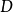 的质心。
的质心。 的质心与具有相同密度的相同形状的物理板的重心重合1。
的质心与具有相同密度的相同形状的物理板的重心重合1。
相关术语垂直轴定理
平行轴定理
惯性矩
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国