[科普中国]-动基床反力法

动基床反力法又称为弹性基床反力法，计算地基土上负荷结构的挠曲的一种方法就是用一组独立的弹簧来代替地基土，而弹簧变形时能产生同样的反力。这一概念叫做弹性基床反力理论，并曾在诸如林(Hayashi)(1921)、太沙基(1943)和赫坦伊(1946)等人的著作中讨论过，太沙基(1955)还对确定弹性基床反力系数的方法进行过详尽的论述。1

计算公式对于一个给定的体系，基床反力系数和弹簧常数的关系为：

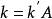式中弹簧常数k为基床反力系数k′(或引起单位位移所需的压力)与基础面积A的乘积。所以,如果能获得有关作用荷载与位移的试验资料,就可算出k值,并从上式求出k′。

根据载荷试验和基础的现场试验资料，可以确定机器基础的k值。巴尔坎(1962)曾引用了大量野外试验资料，证明动弹簧常数实质上等于静反复载荷试验中荷载增量与变形增量(或力矩增量与转角增量)之比。他把从基础块上的动力试验所测得的共振频率与计算所得的无阻尼固有频率进行了比较。计算中采用了基础块加机器的总质量以及从同一基础的静反复载荷试验所测出的k值。根据在砂土、粘土或黄土上，基础面积从5~161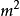。所得的15个试验数据，他发现实测频率平均为计算频率的97%，而极限值从85%到121%。 1

相关概念巴尔坎方法巴尔坎方法的关键是利用静反复载荷试验。此外, “恒载"和“活荷载”的数值应与预计作用在实际基础上的数值相近，这一点也是重要的。因为预期的振动很小,所以不容易从模型基础或原型基础中获得可靠的荷载—变形资料。 这些测试通常要用专门的仪器， 并在做试验时特别细心。

从模型基础试验得到野外试验数据之后，下一步工作就是把这些资料外推到原型尺寸的基础上去。太沙基(1955)和其他人有关静荷载下选择基床反力系数的论述，也适用于动力机器基础的问题中。太沙基(1955)给出了外插试验数据的建议方法。对于竖向振动，它们可表示如下：

对粘性土：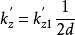

对无粘性图：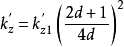

式中：

2d：梁宽或基础底面的短边。

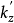:基础短边为2d时的竖向基床反力系数;

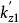:基础短边为1时的竖向基床反力系数。

因此,试验数据提供了资料以确定单位尺寸的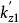值,再应用上式把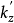调整为原型尺寸基础的基床反力系数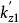。这种方法只有当模型基础和原型基础在相同的土中都产生同等的应力时オ是合理的。1

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所