[科普中国]-位似法作图

利用位似变换的性质解作图题的方法，叫做位似法，位似法作图，常先舍弃图形的大小、位置条件（或部分位置条件），作出满足形状要求的图形F'，然后选择适当的位似中心和位似比，作出符合大小要求（或位置要求），并与F'位似的图形F1。

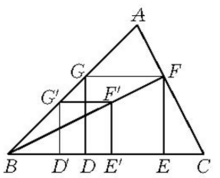
基本介绍位似法作图(construction with homothetic method)是一种常用的作图方法，利用位似变换的方法作图。要作出满足某些条件的图形，可以先放弃一两个条件，作出与其位似的图形，然后利用位似变换，将这个与其相似的图形放大或缩小，以满足全部条件，从而作出所要求作的图形。例如，要求作锐角三角形ABC的内接正方形DEFG，先放弃一个顶点F在边AC上的条件，作出与正方形DEFG位似的正方形D′E′F′G′(如图1)，然后利用位似变换将正方形D′E′F′G′放大，以满足全部条件，从而求得所要作的正方形DEFG2。

例题解析【例1】在已知半圆内求作内接矩形，使矩形的一边在半圆直径上，并且相邻边之比等于定比1。

已知 以AB为直径的半圆O，线段m,n。

求作 矩形EFGH，使EF在AB上，点G，H在圆弧上，并且

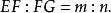
分析 因为“矩形邻边之比为定比m:n”这一条件决定了矩形的形状，而内接于半圆的位置条件决定了矩形的大小，于是先作出符合形状要求的矩形E'F'G'H'，然后以圆心O为位似中心，作出与E'F'G'H'位似的内接于半圆的矩形。

作法 (1)以O为中点，在AB上作线段E'F'，使E'F'=m。

(2)以E'F’为一边，作矩形E'F'G'H'，使F'G'=n(如图2)。

(3)连OG'，OH'，设交半圆于点G，H。

(4)连GH，过点G，H作AB的垂线，垂足分别是F，E。

则EFGH为所求作的矩形。

证明 略。

讨论 本题恒有一解.

【例2】已知三角形的两内角以及两角夹边与高的和，求作三角形。

已知 角a,β，线段l。

求作 △ABC，使∠A=a，∠B=β，高CD与AB的和为l。

分析 ∠A=a，∠B=β 是△ABC的形状条件，CD+AB=l是决定△ABC大小的条件。

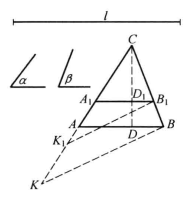
先作出符合形状要求的图形△CA₁B₁，使∠A₁=α，∠B₁=β，以点C为位似中心作△CA₁B₁的位似△ABC，下面决定位似比。

因为

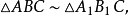所以

则

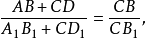即

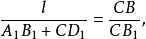这样，点B可确定，点A亦随之可定。

作法 (1)作△A₁B₁C，使∠A₁=α，∠B₁=β，再作A₁B边上的高CD₁(如图3)。

(2)在射线CA₁上取CK₁=CD₁+ A₁B₁，取CK=l。

(3)连K₁B₁，过点K作K₁B₁的平行线交CB₁于点B。

(4)过点B作A₁B₁的平行线交CA₁于点A。

则△ABC为所求1。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学