[科普中国]-面积割补法作图

面积割补法作图(construction by excision and fill vacancy area)是作图解题的一种常用方法。关于面积的作图，多数是等积变形的问题，就是要改变直线形的形状，但不许改变它的面积。这种问题除一部分须用代数解析外，通常可应用定理“两三角形同底而顶点都在底的一条平行线上，那么一定等积”，就是“同底等高的两三角形等积”，在原形上割下一三角形，再利用平行线补以同底等高的另一三角形，使面积不变，而成所需的另一形状。打一个比方，好象沿江的沙滩，受到暴风雨的侵袭，往往西沙塌掉一块，东沙涨起一块，地形虽变，但面积不变。这样的作图方法叫做面积割补法。

基本介绍面积割补法作图是作图解题的一种常用方法。对于等积变形的作图题，通常在给定图形或某一确定图形上割下一个三角形，再借助平行线补上一个同底等高的另一个三角形，使面积不变，从而完成所求作图形。

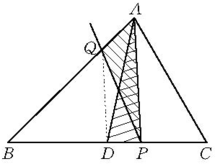
例如，过△ABC的底边BC上一定点P求作一条直线，使它分△ABC的面积为相等的两部分。其思路要点是：因为中线AD平分△ABC的面积，所以首先作中线AD，假设PQ平分△ABC的面积(如图1)，在△ADC中，割去△APD，再补上△APQ，由于△APD与△APQ同底等高，面积相等，所以符合条件的PQ可以作出，本题一解1。

例题解析【例1】如图，在四边形ABCD中，DE是与BC相交的直线，在BC的延长线上求作一点F，使△DEF的面积等于四边形ABCD的面积2。

作法(1)连结BD，过点A作AG//BD，交CB的延长线于G，连结DG；

(2)延长BC到F，使CF=EG，连结DF，

则△DEF就是所求作的三角形。

证明和讨论略。

说明 本题是应用“面积割补法”作图的，根据同底等高的两个三角形面积相等的性质，把△BAD等积变形为△BGD，再根据等底同高的两个三角形面积相等的性质，把△DGE等积变形为△DCF，在解题过程中用了两种不同的等积变形的方法。

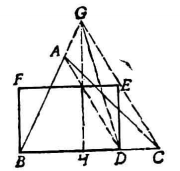
【例2】求作一矩形使和已知三角形等积，且使矩形的一边等于定长l3。

分析 先把△ABC等积变形为底等于l的△GBD，然后再以△GBD的底为长，高的一半为宽，作矩形即可。．

作法 在BC(或其延长线)上取BD=l，连AD，过点C作AD平行线交BA(或其延长线)于点G；过点G作GH⊥BD，垂足为H；再以BD为长、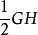为宽作矩形BDEF，则矩形BDEF即为所求。

证略。

【例3】把一个已知四边形ABCD改成一个等积的矩形，使矩形的底等于定长l。

分析 先把四边形ABCD改成一个等积三角形，然后解之。

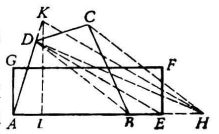
作法 连BD，过点C作BD平行线交AB延长线于点H，在AH(或其延长线)上取AE=l，过点H作HK∥DE，交AD延长线于点K，过点KL⊥AE，垂足为L。再以AE为长、 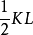为宽作矩形AEFG，则矩形AEFG即为所求。

证略3。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学