[科普中国]-月形定理

月形定理(lunar theorem)是勾股定理的推广，以直角三角形的两直角边为直径分别向形外作半圆，再用直角三角形的外接(半)圆截这两个半圆而成的两个月形面积的和等于该直角三角形的面积。月形定理实际上是把“直角三角形斜边上图形的面积等于两直角边上相似图形面积的和”用在半圆上，它最先是由希俄斯的希波克拉底(Hippocrates，(C))提出来的，所以也称希波克拉底定理，他用此定理去研究化圆为方问题，由于他的疏忽，而用了不正确的推论，以致有一时期有人误认为化圆为方的问题已经解决，实际上化圆为方是一个尺规作图不能问题1。

基本介绍定理直角三角形直角边上两个月形面积之和，等于直角三角形的面积(图1)。

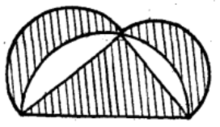
这个定理是希腊著名几何学家希波克拉图(Hippocrates)(也译作“希波克拉底”等)提出来的。其证明并不复杂2。

月形定理的证明设直角三角形两直角边为a，b，斜边为c，两月形面积为S₁，S₂，三角形面积为S。

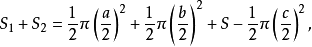
希波克拉图在几何学上贡献颇大，他的《几何纲要》是第一本几何教科书，欧几里德的《几何原本》就是以它为蓝本的。现在几何中将字母注于图形上， 如点日A，直线日AB等，相传为希氏创始而为后世所沿用。希氏曾致力于“化圆为方”和“立方倍积”问题的研究，月形定理是其之出发点，由于他的疏忽，曾使人们一度认为化圆为方十分容易，不少人上了当。他把月形定理应用到正方形上，得出正方形边上两个月形面积之和等于该正方形面积之半的结论(图2)，这显然是正确的。既然圆的内接正方形有这样的性质，那么圆内接正六边形“当然”也就有类似性质：正六边形三边上月形面形之和等于正六边形的面积之半。希氏没有发现这种“想当然”的结论是不正确的，进而应用这个错误定理引出了更错误的结论：圆可以化为方！请看他的推理过程(图3)2：

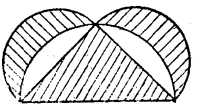
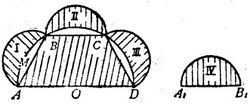
设AB是圆内接正六边形的一边，A₁B₁=AB，直径为AD的半圆面积，等于直径分别为AB、BC、CD和A₁B₁的四个半圆面积之和(请读者自己验证)。

S梯形ABCD= 4S直径为AB的半圆一3S弓形AMB

= 4SⅣ一3S弓形AMB=SⅣ+ 3(SⅣ-S弓形AMB)

=SⅣ+ 3S月形。

所以SⅣ=S梯形ABCD一3S月形。

既然假定月形Ⅰ、Ⅱ、 Ⅲ，能够化成正方形，那么半圆Ⅳ也可化成正方形，这显然是错误的。

应该承认希氏解决问题的方法是有天才的。但由于命题的假设未经一般的证明，所以得出了错误的结论，这个实例，对我们学习数学的青年人是很有借鉴作用的2。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所