[科普中国]-旋转法作图

通过旋转图形使旋转后的图形与原来的图形建立起某些联系，即通过图形位置的变化，把条件不甚明显的量之间的关系转化为明显的量的关系，以利于探索出证题的途径，这种方法就叫做旋转法。旋转法虽然是处理几何问题的一种重要思考方法，但是在运用旋转法时要具体问题具体分析，要以使所证问题简便为准则1。

基本介绍旋转法作图(construction by rotation)是作图题解的一种方法，有些作图题，需要将某些几何元素或图形绕某一定点旋转适当角度，以使已知图形与所求图形发生联系，从而发现作图途径。

例如，已知三条平行线求作一个正三角形，使三个顶点分别在这三条平行线上，其思路要点是：假设△ABC是正三角形，且顶点A，B，C分别在直线a，b，c上，作AD⊥b，将△ABD绕A点逆时针旋转60°后置于△ACD′的位置，此时，点D′可以确定，从而C点亦可确定，再作∠BAC=60°，B点又可确定，故符合条件的正三角形可以作出(如图1)，若不考虑正△ABC的具体位置，而只考虑三个顶点分别在三条平行线上，则此题只有一解2。

例题解析【例1】已知：E是正方形ABCD的BC边上任意一点，∠EAD的平分线AF与CD交于F，求证：DF=AE-BF。

证明：如图2所示。

以A为中心，把△ADF旋转90°，使∠ADF转到△ABG的位置。

∵AD=AB，

∴AD与AB重合。

又∠D=∠ABG=90°，

显然BG与BC在一条直线上。

∵∠GAB=∠DAF=∠FAE，

∴∠GAE=∠BAF=∠AFD=∠AGB，

∴AE=GB+BE=DF+ BE，

即DF=AE-BF1。

【例2】已知：平行四边形ABCD，分别以AB、BC为边向平行四边形内侧作正三角形ABE和BCF。求证：△DEF是正三角形。

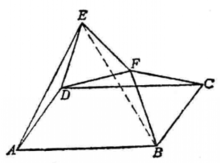
证明： 如图3所示。以F为中心，把△FDC按顺时针方向旋转60°，则FC变到FB位置。

∵CD//AB且CD=AB，∠EBA=60°，

∴CD变到BE位置，FD= FE，

且 ∠DFE= 60°，

∴△DEF是正三角形。

以上旋转都是以三角形为基础进行旋转的。根据具体问题，还可能以正方形或其它一些任意图形为基础进行旋转；而旋转的度数可能是90°、60° 或其它任意度数；因此，采用这种方法证题时，要具体问题具体分析1。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学