[科普中国]-粒子滤波器

粒子滤波器(particle filter)是一种使用蒙特卡罗方法(Monte Carlo method)的递归滤波器，透过一组具有权重的随机样本(称为粒子)来表示随机事件的后验机率，从含有噪声或不完整的观测序列，估计出动态系统的状态，粒子滤波器可以运用在任何状态空间的模型上。

粒子滤波器是卡尔曼滤波器(Kalman filter)的一般化方法，卡尔曼滤波器建立在线性的状态空间和高斯分布的噪声上；而粒子滤波器的状态空间模型可以是非线性，且噪声分布可以是任何型式。

粒子滤波器原理粒子滤波器能够从一系列含有噪声或不完整的观测值中，估计出动态系统的内部状态。在动态系统的分析中，需要两个模型，一个用来描述状态随时间的变化**(系统模型)，另一个用来描述每个状态下观测到的噪声(观测模型)**，将这两个模型都用机率来表示1。

在许多情况下，每得到一个新的观测值时，都必须对系统做出一次估计，利用递回滤波器，能够有效地达到这样的目的。递回滤波器会对得到的资料做连续处理，而非分批处理，因此不需要将完整的资料储存起来，也不需要在得到新的观测值时，将现有的资料重新做处理。递回滤波器包含两个步骤：

预测：利用系统模型，由前一个状态的资讯预测下一个状态的机率密度函数。

更新：利用最新的观测值，修改预测出的机率密度函数。

借由贝叶斯推论(Baysian inference)，我们可以描述出状态空间的机率，并在得到新的观测值时，对系统做出更新，因而达成上述目的。

非线性贝叶斯追踪在动态系统中，我们常常需要对物体做追踪。假设有一动态系统，已知其状态序列 定义为

其中 是状态转移函数，可以是非线性的函数， 是一个**独立且相同分布(i.i.d.)**的过程噪声序列， 和 分别代表状态和过程噪声向量的维度，N为自然数的集合。追踪的目标是要递回地从观测值 估计出 ，而观测值 定义为

其中 是观测函数，可以是非线性的函数， 是一个**独立且相同分布(i.i.d.)**的观测噪声序列， 和 分别代表观测值和观测噪声向量的维度。

从贝叶斯理论的观点来看，追踪问题是要根据到时间k为止的已知资讯 ，递回地计算出时间{k的状态 的可信度，这个可信度用机率密度函数来表示。假设初始机率密度函数 p(x_{0})}(称为先验机率)为已知，则利用**“预测”和“更新”**两个步骤就能递回地计算出机率密度函数 。

在此假设在时间k-1的机率密度函数为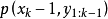 已知。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所