在计算机科学中,二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search),是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
原理计算步骤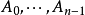 给予一个包含
给予一个包含 个带值元素的数组
个带值元素的数组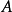 或是记录,使
或是记录,使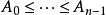 ,以及目标值
,以及目标值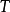 ,还有下列用来搜索
,还有下列用来搜索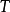 在
在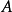 中位置的子程序。
中位置的子程序。
令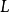 为
为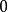 ,
,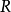 为
为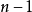 。
。
如果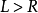 ,则搜索以失败告终。
,则搜索以失败告终。
令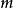 (中间值元素)为
(中间值元素)为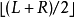 。
。
如果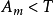 ,令
,令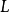 为
为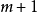 并回到步骤二。
并回到步骤二。
如果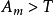 ,令
,令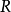 为
为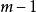 并回到步骤二。
并回到步骤二。
当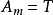 ,搜索结束;回传值
,搜索结束;回传值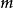 。
。
这个迭代步骤会持续通过两个变量追踪搜索的边界。有些实际应用会在算法的最后放入相等比较,让比较循环更快,但平均而言会多一层迭代。
大致匹配以上程序只适用于完全匹配,也就是查找一个目标值的位置。不过,因为有序数组的顺序性,将二分搜索算法扩展到能适用大致匹配并不是很重要。举例来说,二分搜索算法可以用来计算一个赋值的排名(或称秩,比它更小的元素的数量)、前趋(下一个最小元素)、后继(下一个最大元素)以及最近邻。搜索两个值之间的元素数目的范围查询可以借由两个排名查询(又称秩查询)来运行。
排名查询可以使用调整版的二分搜索来运行。借由在成功的搜索回传{\displaystyle m},以及在失败的搜索回传{\displaystyle L},就会取而代之地回传了比起目标值小的元素数目。
前趋和后继查询可以借由排名查询来运行。一旦知道目标值的排名,其前趋就会是那个位于其排名位置的元素,或者排名位置的上一个元素(因为它是小于目标值的最大元素)。其后继是(数组中的)下一个元素,或是(非数组中的)前趋的下一个元素。目标值的最近邻可能是前趋或后继,取决于何者较为接近。
范围查询也是直接了当的。一旦知道两个值的排名,不小于第一个值且小于第二个值的元素数量就会是两者排名的差。这个值可以根据范围的端点是否算在范围内,或是数组是否包含其端点的对应键来增加或减少1。1
复杂度分析时间复杂度
折半搜索每次把搜索区域减少一半,时间复杂度为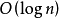 。(n代表集合中元素的个数)
。(n代表集合中元素的个数)
空间复杂度
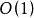 ,虽以递归形式定义,但是尾递归,可改写为循环。
,虽以递归形式定义,但是尾递归,可改写为循环。
示例代码C 版本- 递归int binary_search(const int arr[], int start, int end, int khey) {if (start > end)return -1; int mid = start + (end - start) / 2; //直接平均可能会溢位,所以用此算法if (arr[mid] > khey)return binary_search(arr, start, mid - 1, khey);else if (arr[mid] khey)return this.binary_search(low, mid - 1, khey);if (this[mid] end:return -1mid = start + (end - start) / 2if arr[mid] > hkey:return binary_search(arr, start, mid - 1, hkey)if arr[mid]




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国