[科普中国]-稀疏滤波

稀疏滤波只有一个hyperparameter（需要学习的特征数目）需要调整。但它很有效且与其他的特征学习方法不同，稀疏滤波并没有明确的构建输入数据的分布的模型。它只优化一个简单的代价函数（L2范数稀疏约束的特征），优化过程可以通过几行简单的Matlab代码就可以实现。而且，稀疏滤波可以轻松有效的处理高维的输入，并能拓展为多层堆叠。

简介稀疏滤波方法的核心思想就是避免对数据分布的显式建模，而是优化特征分布的稀疏性从而得到好的特征表达。

一般来说，大部分的特征学习方法都是试图去建模给定训练数据的真实分布。换句话说，特征学习就是学习一个模型，这个模型描述的就是数据真实分布的一种近似。这些方法包括denoising autoencoders，restricted Boltzmann machines (RBMs)，independent component analysis (ICA)和sparse coding等等。

这些方法效果都不错，但缺点就是，他们都需要调节很多参数。比如说学习速率learning rates、动量momentum（好像rbm中需要用到）、稀疏度惩罚系数sparsity penalties和权值衰减系数weight decay等。而这些参数最终的确定需要通过交叉验证获得，本身这样的结构训练起来所用时间就长，这么多参数要用交叉验证来获取时间就更多了。我们花了大力气去调节得到一组好的参数，但是换一个任务，我们又得调节换另一组好的参数，这样就会花了俺们太多的时间了。虽然ICA只需要调节一个参数，但它对于高维输入或者很大的特征集来说，拓展能力较弱。

稀疏滤波一种简单并且有效的特征学习算法，它只需要最少的参数调节。虽然学习数据分布的模型是可取的，而且效果也不错，但是它往往会使学习的算法复杂化，例如：RBMs需要近似对数划分log-partition函数的梯度，这样才可能优化数据的似然函数。Sparse coding需要在每次的迭代过程中寻找活跃的基的系数，这是比较耗时的。而且，稀疏因子也是一个需要调整的参数。本文方法主要是绕过对数据分布的估计，直接分析优化特征的分布。了解最优特征分布需要先关注特征的一些主要属性：population sparsity，lifetime sparsity和high dispersal。怎样的特征才是好的特征，才是对分类或者其他任务好的特征。我们的学习算法就应该学会去提取这种特征。

具体介绍稀疏滤波是如何捕捉到上面说的那些特性的。我们先考虑下从每个样本中计算线性特征。具体来说，我们用 来表示第i个样本（特征矩阵中第i列）的第j个特征值（特征矩阵中第j行）。因为是线性特征，所以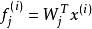 。第一步，我们先简单的对特征矩阵的行进行归一化，然后再对列进行归一化，然后再将矩阵中所有元素的绝对值求和。

具体来说，我们先归一化每个特征为相等的激活值。具体做法是将每一个特征除以其在所有样本的二范数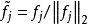： 。然后我们再归一化每一个样本的特征。这样，他们就会落在二范数的单位球体unit L2-ball上面了。具体做法是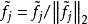： 。这时候，我们就可以对这些归一化过的特征进行优化了。我们使用L1范数惩罚来约束稀疏性。对于一个有M个样本的数据集，sparse filtering的目标函数表示为：

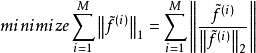
优化样本的稀疏性其中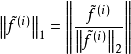 这一项度量的就是第i个样本的特征的population sparsity，也就是限制每个样本只有很少的非零值。因为归一化的特征 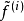被约束只能落在二范数的单位球体上面，所以当这些特征是稀疏的时候，也就是样本接近特征坐标轴的时候，上面的目标函数才会最小化。反之，如果一个样本的每个特征值都差不多，那么就会导致一个很高的惩罚。可能有点难理解，我们看图一：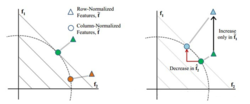

图一左：假设我们的特征维数是两维(f1, f2)，我们有两个样本，绿色和褐色的。每个样本都会先投影到二范数的球体上面（二维的话就是单位圆），再进行稀疏性的优化。可以看到，当样本落在坐标轴的时候，特征具有最大的稀疏性（例如，一个样本落在f2轴上，那么这个样本的表示就是(0, 1)，一个特征值为1，其他的为0，那么很明显它具有最大的稀疏性）。图一右：因为归一化，特征之间会存在竞争。上面有一个只在f1特征上增加的样本。可以看到，尽管它只在f1方向上增加（绿色三角型转移到蓝色三角型），经过列归一化后（投影到单位圆上），可以看到第二个特征f2会减少（绿色圆圈转移到蓝色圆圈）。也就是说特征之间存在竞争，我变大，你就得变小。

对特征进行归一化的一个属性就是它会隐含的进行特征间的竞争。归一化会使得如果只有一个特征分量f增大，那么其他所有的特征分量的值将会减小。相似的，如果只有一个特征分量f减小，那么其他所有的特征分量的值将会增大。因此，我们最小化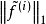 ，将会驱使归一化的特征趋于稀疏和大部分接近于0。也就是，一些特征会比较大，其他的特征值都很小（接近于0）。因此，这个目标函数会优化特征的population sparsity。

优化高扩散性上面说到，特征的high dispersal属性要求每个特征被恒等激活。在这里，我们粗鲁地强制每个特征的激活值平方后的均值相等。在上面sparse filtering的公式中，我们首先通过将每个特征除以它在所有样本上面的二范数来归一化每个特征，使他们具有相同的激活值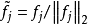： 。实际上，它和约束每个特征具有相同的平方期望值有一样的效果。 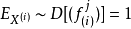，因此，它已经隐含的优化了high dispersal属性。

优化稀疏性我们发现，对population sparsity和high dispersal的优化就已经隐含的优化了特征的lifetime sparsity。这其中的缘由是什么呢。首先，一个具有population sparsity的特征分布在特征矩阵里会存在很多非激活的元素（为0的元素）。而且，因为满足high dispersal，这些零元素会近似均匀的分布在所有的特征里。因此，每一个特征必然会有一定数量的零元素，从而保证了lifetime sparsity。所以，对于population sparsity和high dispersal的优化就已经足够得到一个好的特征描述了。

深度稀疏滤波因为sparse filtering的目标函数是不可知的，我们可以自由地选择一个前向网络来计算这些特征。一般来说，我们都使用比较复杂的非线性函数，例如：

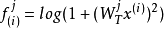
或者多层网络来计算这些特征。这样，sparse filtering也算是训练深度网络的一种自然的框架了。

有sparse filtering的深度网络可以使用有代表性的逐层贪婪算法来训练。我们可以先用sparse filtering来训练得到一个单层的归一化的特征，然后用它当成第二层的输入去训练第二层，其他层一样。实验中，我们发现，它能学习到很有意义的特征表达。1

与divisive normalization的联系sparse filtering的population sparsity和divisive normalization有着紧密的联系。divisive normalization是一种视觉处理过程，一个神经元的响应会除以其邻域所有神经元的响应的和（或加权和）。divisive normalization在多级目标识别中是很有效的。然而，它被当成一个预处理阶段引入，而不是属于非监督学习（预训练）的一部分。实际上，sparse filtering把divisive normalization结合到了特征学习过程中，通过让特征间竞争，学习到满足population sparse的特征表达。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所