[科普中国]-基本轨迹

基本轨迹(elementary locus)是一类常用的轨迹。求各种轨迹时，经常把它归结为求一些简单的已知轨迹，它们就称为基本轨迹。通常使用的基本轨迹有以下六种：1.到定点的距离等于定长的点的轨迹是以定点为圆心，定长为半径的圆；2.和已知线段两个端点的距离相等的点的轨迹是这条线段的垂直平分线；3.与两条相交直线距离相等的点的轨迹是平分这两条直线交角的两条互相垂直的直线；4.到一条已知直线距离等于定长的点的轨迹，是在已知直线两旁平行于这条直线，并且到这条直线的距离等于定长的两条直线；5.与两条平行直线的距离相等的点的轨迹是这两条平行线的公垂线段的垂直平分线；6.和已知线段两个端点连线的夹角等于已知角的点的轨迹，是以已知线段为弦，所含圆周角等于已知角的两段弧(端点除外)。特别地，当和已知线段两端点连线的夹角等于直角时，轨迹便是以已知线段为直径的圆，即两个半圆周合为一个圆周(两个端点除外)1。

基本介绍根据初等几何中已经有的知识，可得下列七个常用的基本轨迹。

设A、B是两个定点(图1)，我们知道，距离A、B两点等远的点P，全在AB的中垂线l上；而且AB的中垂线l上的任何一点，距A、B两点都等远，即l上没有距A、B不等远的点，因此，l是全体距离A、B两点等远的点组成的图形，一个也不多，一个也不少。这是一个基本轨迹2。

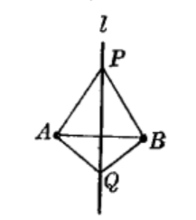
基本轨迹1距离两个已知点等远的点的轨迹，是这两点间所连线段的中垂线2。

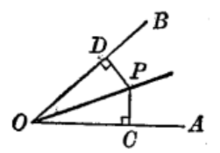
再讨论和一个角的两边等距的点的轨迹(图2)，已知和一个角的两边等距的点，都在这个角的平分线上，而且角平分线上任一点，都同两边等距，据此， 可得基本轨迹2。

基本轨迹2同已知角两边等距的点的轨迹，是这个角的平分线。

注意：说具有某种条件的点的轨迹是某种图形，要从两方面考虑。第一，具有这种条件的点必须都在这个图形上，一个也不能少；第二，这个图形上的点必须都具有这个条件，也就是说，不能多出来不具有这个条件的点。

基本轨迹3同两条平行的已知直线等距的点，是一条直线，它和这两条已知直线平行，且同它们等距。

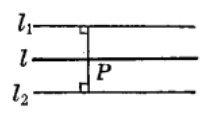
如图3，直线l是同直线l1、l2等距的点的轨迹。自己考虑一下，是否和l1、l2等距的点都在l上?有没有不在l上的点也和l1、l2等距的?另一方面，还要考虑，l上的点有没有距离l1、l2不等的?

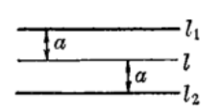
再想一个问题，到一条直线l的距离等于定长a的点的轨迹是什么图形?容易想到，是和l距离为a的平行线。但要注意，在l两侧都有一条(图4)，这是基本轨迹42。

基本轨迹4到一条已知直线距离为定长的点的轨迹，是和已知直线平行的一双直线，其中每一条到已知直线的距离都等于定长。

基本轨迹5到一个定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的一个圆(图5)。

从一点P引出的两条射线，通过一条线段AB的两个端点时，这两条射线所成的角，叫做P点对于线段AB的视角。

基本轨迹6对于一定线段的视角等于定角的点的轨迹，是以定线段为弦的一双弓形弧(图6)。

在轨迹6中，定角是直角时，两个弓形弧都是半圆，它们合成一个整圆，这是:

基本轨迹7对于一定线段的视角等于直角的点的轨迹，是以定线段为直径的一个圆(图7)。

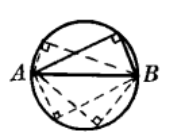
初等几何中只研究轨迹是直线或圆的情形、以上七个基本轨迹，是分析其他轨迹问题的基础2。

例题解析【例1】 求过圆内一点的弦的中点的轨迹。

解:轨迹就是按照一定条件运动的点经过的路线，求轨迹时，先要按照条件画出动点，画画看。

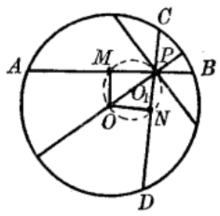
如图8, P是⊙O内一个定点，过P点作弦，绕P点旋转，看这动弦中点经过什么路线，可以看出，如图中虚线，可能是个圆。

究竟是不是圆呢?如果是，圆心在哪里，半径多大?这要具体分析。

设AB是任意一条过P点的弦，看AB的中点M有什么性质，

∵AM= MB， ∴OM⊥AB，

即∠OMP是直角。这就是说，过P点的任意一条弦的中点M，对于线段OP的视角等于直角。因此，全体过P点的弦的中点，都在以OP为直径的圆周上。

作出以OP为直径的圆⊙O1(图中虚线)，所求轨迹是不是这个圆周呢?还要看⊙O1上有没有不合条件的点。

在⊙O1上任取一点N，连ON，作PN⊥ON，交⊙O于C、D，那么N是CD弦的中点，这说明⊙O1上任何一点都是一条过P点的弦的中点，没有不符合条件的点。

结果得，过圆内一定点的弦的中点的轨迹，是以圆心和这定点的连线为直径的一个圆。

有个特殊情况：如果定点P就是圆心O，过P点的弦都是直径，它们的中点都是O点，这时，轨迹只是O点一个点2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学