[科普中国]-欧拉﹣伯努力栋梁方程

欧拉-伯努利梁方程（英语：Euler–Bernoulli beam theory），是一个关于工程力学、经典梁力学的重要方程；是一个简化线性弹性理论用于用于计算梁受力和变形特征。欧拉-伯努利梁方程约形成于1750年，但这条方程却没有在后期建筑之中得到广泛的应用。直到十九世纪，这条方程才成为第二次工业革命的基石。

简介欧拉-伯努利梁方程（英语：Euler–Bernoulli beam theory），是一个关于工程力学、经典梁力学的重要方程；是一个简化线性弹性理论用于用于计算梁受力和变形特征。欧拉-伯努利梁方程约形成于1750年，但这条方程却没有在后期建筑之中得到广泛的应用。直到十九世纪，这条方程才成为第二次工业革命的基石。1

历史普遍认为，伽利略是提出关于梁的重要理论的第一人，但是近代史家发现，达芬奇才是第一位研究梁的科学家。但是由于当时缺乏建材弹性的研究和数学基础（主要是微积分），导致伽利略等的科学家没有成功取得突破。1750年，瑞士学者莱昂哈德·欧拉（Leonhard Euler）与丹尼尔·伯努利（Daniel Bernoulli）开始研究梁并把梁理论推向实用，成功地把科学与工程学区分成两个学科，同时使得工程学成为了一门数理科学。1

欧拉-伯努力梁方程欧拉─伯努利梁方程内容描述了梁的位移与载重的关系：

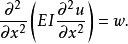其中：为位移，为梁的斜率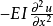，为梁的弯矩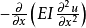，是梁的剪力。1

弹性 (物理学)在物理学中，弹性（来自希腊语ἐλαστός“可塑性”）是指物体受到外力时变形，并且当该外力解除时恢复其初始形状的能力。 固体物体受到外力时将变形。如果材料是弹性的，当这些力被移除时，物体将返回到其初始形状。 弹性是物体具有的一项物理性质。如果一种材料在应力下发生形变，应力撤销后又恢复到原来的形状，这种材料被称为具有弹性。形变的大小称为应变。2

参见硬度

弹性模量

线性弹性

3-D 弹性

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学