[科普中国]-反演法作图

反演法作图(construction by inversion trans-formation)是解作图题的一种特殊方法，就是利用反演变换的性质(如过反演中心的圆变为直线，保角性等)来解作图题的方法，叫做反演法。反演法常用于与圆有关的一类作图题。用反演法作图，关键在于反演中心与反演幂的选取，为了使作图简便，反演幂常常取为反演中心对某个圆的圆幂，在这种情况下，该圆的反形就是自身。

基本介绍对一些作图题，可借助反演变换的性质发现作图途径，将比较复杂的问题转化为已知的或简单的问题，从而得出作图方法。

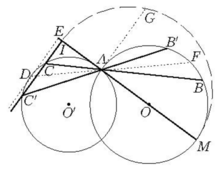
例如，过⊙O和⊙O′的交点A，求作割线BAC，分别割两圆于点B，C，使AB与AC的乘积的绝对值等于k2。本题的思路要点是：假设割线BAC已作出，由AB·AC=k2知，点C必在⊙O的反演图上，同时点C又在⊙O′上，以点A为⊙O的反演中心，则⊙O的反演图为垂直于OA的直线，且AI·AM=k2，点I就可以确定了。自点I作AI的垂直线(就是⊙O的反演圆)，交⊙O′于点C，CAB即为所求(如图1)。本题通常有两解，即BAC和B′AC′，k2有它的最大限，当⊙O的反演图与⊙O′相切时(图中ED位置)，则AI达到它的极大值AE，从而有AM·AE=k2，这时本题只有一解DAF，若k2>AM·AE，则⊙O的反演图与⊙O′不相交，本例无解1。

例题分析【例1】求作一圆，使它通过一已知点且切于两已知圆。

已知 点P及圆O1，圆O2。

求作 圆O，使圆O过点P且与圆O1，圆O2相切。

分析 假定圆O已作出，它过点P，且与圆O1，圆O2相切于点T1，T2(如图2)，如果以P为反演中心，点P到圆O1的圆幂为反演幂进行反演变换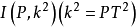，则

圆O1→圆O'1，圆O2→圆O'2，T1→T'1，T2→T'2，圆O→T'1T'2。

由保角性知道，T'1T'2与圆O1，圆O'2相切，于是，原作图题转变为作圆O2的反形圆O'2及圆O1，圆O'2的公切线。

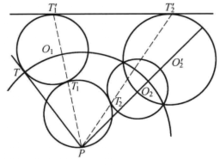
作法 (1)以P为反演极，点P关于圆O1的圆幂(图2中的PT2)为反演幂作圆O2的反形圆O'2。

(2)作圆O1与圆O'2的公切线，设切点分别为T'1，T'2。

(3)连PT'1，PT'2，分别交圆O1，圆O2于点T1，T2。

(4)过点P，T1，T2作圆O。

则圆O为所求。

证明 略。

讨论 由圆O1，与圆O'2有无公切线，以及公切线的条数分析，本题至多有四解。

用反演法作图，关键在于反演中心与反演幂的选取，为了使作图简便，反演幂常常取为反演中心对某个圆的圆幂，在这种情况下，该圆的反形就是自身2。

【例2】过一已知点作一圆，使之切于一已知圆且正交于另一已知圆。

已知 点P，圆O1，圆O2。

求作 圆O，使之过点P，与圆O1相切且与圆O2正交。

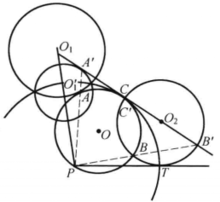
分析 设圆O过点 P，与圆O1相切于点A，与圆O2正交，交点为B,C(如图3)，那么，不妨以点P为反演中心，点P到圆O2的圆幂为反演幂施行反演变换，于是

圆O1→圆O'1，圆O2→圆O'2，

A→A'，B→B'，C→C',

圆O→直线A'B'C'

由保角性知，直线A'B'C'与圆O'1相切于点A'，且过圆O2的圆心。这样，原作图题转化为作出圆O1的反形圆O'1以及过点O2作圆O'1的切线。

作法 (1)以点P为反演中心，点P到圆O2的圆幂为反演幂，作出圆O1的反形圆O'1。

(2)过点O2作圆O'1的切线，设此切线交圆O2于点B'，C' ，与圆O'1切于点A'。

(3)连PA'，PB'，设分别与圆O1，圆O2交于点A，B。

(4)过点P，A，B作圆O。

则圆O为所求作的图形。

证明与讨论 略2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学