[科普中国]-轨迹交点法

如果解决一个作图题归结起来是要确定某一个点的位置，可以暂时放弃这点所应满足的条件之一，这时满足其余条件的点可形成一个轨迹；再改换放弃另一个条件，又得到一个轨迹，所求的点应在这两个轨迹上，因此，两个轨迹的交点就是所求作的点，像这样利用轨迹的交点来解作图题的方法，叫做轨迹交点法或轨迹交接法或径称轨迹法1。

基本介绍轨迹交点法(method of intersection point of locus)是解作图题的一种重要方法，解作图题常归结到确定某一点的位置，如果这个点的位置是由两个条件确定的，先放弃其中一个条件，那么这个点的位置就不定而形成一个轨迹；若改换放弃另一个条件，这个点就在另一个轨迹上，故此点便是两个轨迹的交点，这种利用轨迹的交点来解作图题的方法称为轨迹交点法，或称为交轨法、轨迹交截法、轨迹法。用这种方法来作图，称为轨迹法作图。

例如，设⊙O与⊙O′相离，半径分别为R与R′，求作半径为r的圆，使其与⊙O及⊙O′外切，该作图题的思路要点是：设⊙M是合条件的圆，即其半径为r并与⊙O及⊙O′外切(如图1)，显然，M点是由两个轨迹确定的，即M点既在以O为圆心以R+r为半径的圆上，又在以O′为圆心以R′+r为半径的圆上，因而所求圆的圆心位置可确定，于是该作图题可以求解。若⊙O与⊙O′相距为b，当2rb时，有两解2。

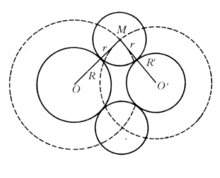
轨迹交点法在作图中应用广泛，凡属作图，几乎没有不用到它的。这是因为我们所使用的工具——直尺和圆规的作图在本质上就体现了求轨迹交点的作用。正因如此，轨迹交点法可说就是其他作图方法的基础。

有时欲确定的某一个点已明确指出系在某已知图形上，那么只要求出一个轨迹就可以了，这种情形叫做单轨法。如果并未指出在某已知图形上，需要求出两个轨迹才能确定所求点的位置，这种情形叫做双轨法。

能确定某一个点的轨迹常常有若干个，为使作图简捷，我们应该注意选择那些便于作出的轨迹2。

例题解析【例1】 已知一边及这边上的中线和高，作三角形。

已知：线段a、m、h，求作：△ABC，使BC=a，中线AD=m，高AE=h。

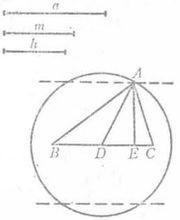
分析：假设△ABC已作出，其中BC=a，中线AD=m，高AE=h，BC=a，如果A点可定，这个作图题就可解，A点适合两个条件：1．和BC的中点的距离等于m；2．和BC的距离等于h。若利用第一个条件，先放弃第二个条件，可得以BC的中点为圆心，m为半径的圆；再利用第二个条件而放弃第一个条件，得出仅适合于第二个条件的点的轨迹，是和BC平行且距离等于h的两条直线。所求的A点就是这两个轨迹的交点(图2)1。

作法：

1．作BC=a。

2．取BC的中点D，以D为圆心，m为半径作圆。

3．作和BC平行并且距离等于h的直线交圆于A。

4．连结AB和AC。

△ABC就是所求作的三角形。

讨论：

1.当h>m时，两个轨迹没有交点，这时无解。

2.当h=m时，两个轨迹相切，有两个切点，这时可以作出两个三角形，但它们是全等的。

3.当h