[科普中国]-周期性神经网络

周期性神经网络（RNN）又称时间递归神经网络。时间递归神经网络的神经元间连接构成矩阵。RNN一般指代时间递归神经网络。单纯递归神经网络因为无法处理随着递归，权重指数级爆炸或消失的问题（Vanishing gradient problem），难以捕捉长期时间关联；而结合不同的LSTM可以很好解决这个问题。

简介时间递归神经网络可以描述动态时间行为，因为和前馈神经网络（feedforward neural network）接受较特定结构的输入不同，RNN将状态在自身网络中循环传递，因此可以接受更广泛的时间序列结构输入。手写识别是最早成功利用RNN的研究结果。

在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNNs之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。理论上，RNNs能够对任何长度的序列数据进行处理。

原理介绍编码器递归神经网络将输入序列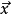 编码为一个固定长度的隐藏状态 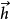，这里有（用自然语言处理作为例子）：

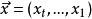是输入序列，比如编码为数字的一系列词语，整个序列就是完整的句子。

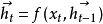是随时间更新的隐藏状态。当新的词语输入到方程中，之前的状态 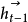就转换为和当前输入 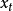相关的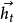 ，距离当前时间越长，越早输入的序列，在更新后的状态中所占权重越小，从而表现出时间相关性。

其中，计算隐藏状态的方程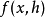 是一个非线性方程，可以是简单的Logistic方程（tanh），也可以是复杂的LSTM单元（Long-Short Term Memory）。而有了隐藏状态序列，就可以对下一个出现的词语进行预测：

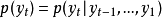，其中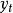 是第t个位置上的输出，它的概率基于之前输出的所有词语。

以上概率可以通过隐藏状态来计算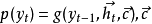： 是所有隐藏状态的编码，总含了所有隐藏状态，比如可以是简单的最终隐藏状态 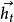，也可以是非线性方程的输出 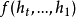。因为隐藏状态t就编码了第t个输入前全部的输入信息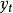， 也迭代式地隐含了之前的全部输出信息，所以这个概率计算方法是合理的。

这里的非线性方程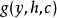 可以是一个复杂的前馈神经网络，也可以是简单的非线性方程（但有可能因此无法适应复杂的条件而得不到任何有用结果）。给出的概率可以用监督学习的方法优化内部参数来给出翻译，也可以训练后用来给可能的备选词语，用计算其第j个备选词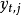当前的下一位置的概率，给它们排序。排序后用于其它翻译系统，可以提升翻译质量。

解码器更复杂的情况下复发神经网络还可以结合编码器作为解码器（Decoder），用于将编码后（Encoded）的信息解码为人类可识别的信息。也就是上述例子中的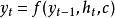 过程，当中非线性模型 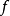就是作为输出的复发神经网络。只是在解码过程中，隐藏状态因为是解码器的参数，所以为了发挥时间序列的特性，需要对 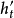继续进行迭代：

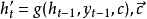是解码器传递给编码器的参数，是解码器中状态的summary。 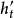是解码器的隐藏状态。 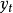是第t个输出。

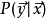当输入仍为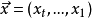 ，输出是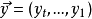 ，最大化条件概率后就是最好的翻译结果。

双向读取用两个复发神经网络双向读取一个序列可以使人工智能获得“注意力”。简单的做法是将一个句子分别从两个方向编码为两个隐藏状态，然后将两个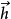 拼接在一起作为隐藏状态。这种方法能提高模型表现的原因之一可能是因为不同方向的读取在输入和输出之间创造了更多短期依赖关系，从而被RNN中的LSTM单元（及其变体）捕捉，例如在实验中发现颠倒输入序列的顺序（但不改变输出的顺序）可以意外达到提高表现的效果。1

实例基于TensorFlow，搭建一个RNN，神经网络进行二进制加法。

import tensorflow as tfimport numpy as np# 一个字典，隐射一个数字到其二进制的表示# 例如 int2binary[3] = [0,0,0,0,0,0,1,1]int2binary = {} # 最多8位二进制binary_dim = 8 # 在8位情况下，最大数为2^8 = 256largest_number = pow(2,binary_dim) # 将[0,256)所有数表示成二进制binary = np.unpackbits( np.array([range(largest_number)],dtype=np.uint8).T,axis=1) # 建立字典for i in range(largest_number): int2binary[i] = binary[i] def binary_generation(numbers, reverse = False): ''' 返回numbers中所有数的二进制表达， 例如 numbers = [3, 2, 1] 返回 ：[[0,0,0,0,0,0,1,1], [0,0,0,0,0,0,1,0], [0,0,0,0,0,0,0,1]' 如果 reverse = True, 二进制表达式前后颠倒， 这么做是为训练方便，因为训练的输入顺序是从低位开始的 numbers : 一组数字 reverse : 是否将其二进制表示进行前后翻转 ''' binary_x = np.array([ int2binary[num] for num in numbers], dtype=np.uint8) if reverse: binary_x = np.fliplr(binary_x) return binary_x def batch_generation(batch_size, largest_number): ''' 生成batch_size大小的数据，用于训练或者验证 batch_x 大小为[batch_size, biniary_dim, 2] batch_y 大小为[batch_size, biniray_dim] ''' # 随机生成batch_size个数 n1 = np.random.randint(0, largest_number//2, batch_size) n2 = np.random.randint(0, largest_number//2, batch_size) # 计算加法结果 add = n1 + n2 # int to binary binary_n1 = binary_generation(n1, True) binary_n2 = binary_generation(n2, True) batch_y = binary_generation(add, True) # 堆叠，因为网络的输入是2个二进制 batch_x = np.dstack((binary_n1, binary_n2)) return batch_x, batch_y, n1, n2, add def binary2int(binary_array): ''' 将一个二进制数组转为整数 ''' out = 0 for index, x in enumerate(reversed(binary_array)): out += x*pow(2, index) return out设置参数batch_size = 64# LSTM的个数，就是隐层中神经元的数量lstm_size = 20# 隐层的层数lstm_layers =2定义输入输出# 输入，[None, binary_dim, 2],# None表示batch_size, binary_dim表示输入序列的长度，2表示每个时刻有两个输入x = tf.placeholder(tf.float32, [None, binary_dim, 2], name='input_x') # 输出y_ = tf.placeholder(tf.float32, [None, binary_dim], name='input_y')# dropout 参数keep_prob = tf.placeholder(tf.float32, name='keep_prob')建立模型# 搭建LSTM层（看成隐层）# 有lstm_size个单元lstm = tf.contrib.rnn.BasicLSTMCell(lstm_size)# dropoutdrop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)# 一层不够，就多来几层def lstm_cell(): return tf.contrib.rnn.BasicLSTMCell(lstm_size)cell = tf.contrib.rnn.MultiRNNCell([ lstm_cell() for _ in range(lstm_layers)]) # 初始状态，可以理解为初始记忆initial_state = cell.zero_state(batch_size, tf.float32) # 进行forward，得到隐层的输出# outputs 大小为[batch_size, lstm_size*binary_dim]outputs, final_state = tf.nn.dynamic_rnn(cell, x, initial_state=initial_state) # 建立输出层weights = tf.Variable(tf.truncated_normal([lstm_size, 1], stddev=0.01))bias = tf.zeros([1]) # [batch_size, lstm_size*binary_dim] ==> [batch_size*binary_dim, lstm_size]outputs = tf.reshape(outputs, [-1, lstm_size])# 得到输出, logits大小为[batch_size*binary_dim, 1]logits = tf.sigmoid(tf.matmul(outputs, weights))# [batch_size*binary_dim, 1] ==> [batch_size, binary_dim]predictions = tf.reshape(logits, [-1, binary_dim])损失函数和优化方法cost = tf.losses.mean_squared_error(y_, predictions)optimizer = tf.train.AdamOptimizer().minimize(cost)训练steps = 2000with tf.Session() as sess: tf.global_variables_initializer().run() iteration = 1 for i in range(steps): # 获取训练数据 input_x, input_y,_,_,_ = batch_generation(batch_size, largest_number) _, loss = sess.run([optimizer, cost], feed_dict={x:input_x, y_:input_y, keep_prob:0.5}) if iteration % 1000 == 0: print('Iter:{}, Loss:{}'.format(iteration, loss)) iteration += 1 # 训练结束，进行测试 val_x, val_y, n1, n2, add = batch_generation(batch_size, largest_number) result = sess.run(predictions, feed_dict={x:val_x, y_:val_y, keep_prob:1.0}) # 左右翻转二进制数组。因为输出的结果是低位在前，而正常的表达是高位在前，因此进行翻转 result = np.fliplr(np.round(result)) result = result.astype(np.int32) for b_x, b_p, a, b, add in zip(np.fliplr(val_x), result, n1, n2, add): print('{}:{}'.format(b_x[:,0], a)) print('{}:{}'.format(b_x[:,1], b)) print('{}:{}\n'.format(b_p, binary2int(b_p)))运行结果Iter:1000, Loss:0.012912601232528687Iter:2000, Loss:0.000789149955380708[0 1 0 1 0 0 1 0]:82[0 0 1 1 1 1 0 0]:60[1 0 0 0 1 1 1 0]:142 [0 1 1 1 1 1 0 0]:124[0 1 1 0 0 0 1 0]:98[1 1 0 1 1 1 1 0]:222.........[0 0 0 0 0 0 1 0]:2[0 1 0 1 0 0 0 0]:80[0 1 0 1 0 0 1 0]:82分类完全递归网络（Fully recurrent network）

Hopfield网络（Hopfield network）

Elman networks and Jordan networks

回声状态网络（Echo state network）

长短记忆网络（Long short term memery network）

双向网络（Bi-directional RNN）

持续型网络（Continuous-time RNN）

分层RNN（Hierarchical RNN）

复发性多层感知器（Recurrent multilayer perceptron）

二阶递归神经网络（Second Order Recurrent Neural Network）

波拉克的连续的级联网络（Pollack’s sequential cascaded networks）

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所