[科普中国]-二级曲线

二级曲线(two class curve)是二次曲线的一种表示方法，即用线坐标表示的二次曲线。当直线ux+vy+w=0的系数u，v，w满足实系数二次方程Au²+2Huv+Bv²+2Guw+2Fvw+Cw²=0(式中(A，B，H)≠(0，0，0))时，这些直线的包络线称为二级曲线，它与二次曲线在本质上是一样的1。

基本概念二级曲线(two class curve)是平面射影几何研究的基本对象，若平面上直线的齐次坐标为[u1，u2，u3]，则满足三元二次齐次方程

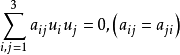的直线的全体称为二级曲线。这里aij为实数且至少有一个不是零，该方程称为二级曲线的方程，(aij)称为系数矩阵。若系数矩阵的行列式|aij|≠0，则二级曲线称为非退化的，否则称为退化的、退化的二级曲线是两个点。在射影平面上，成射影对应的两个点列对应点的连线的集合是二级曲线1。

二级曲线的方程在射影平面上，配极变换的自共轭直线的集合称为二级曲线2。

对于给定的配极变换，即

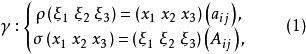
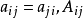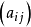其中 是在 中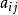 的代数余子式。易得 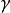对应的二级曲线的方程。

配极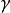 对应的二阶曲线 的方程是

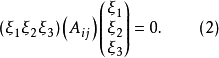就是

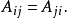
若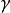 是双曲型的，则它有无穷多条自共轭直线，于是双曲型配极对应的二级曲线有无穷多实直线，有时也将它称为二次线束，见图1。

若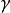 是椭圆型的，则它无自共轭直线，于是椭圆型配极对应的二级曲线不存在，或说对应虚二级曲线。

通过矩阵，配极变换与二阶曲线(或二级曲线)有着一种对应关系：双曲型配极对应实曲线；椭圆型配极对应虚曲线。因此，可以从有关配极的一些概念出发，通过“翻译”，建立有关曲线的对应概念。不过，人们常常关心的是有实图形存在的情况，因此，我们只就双曲型配极对应的曲线讨论之。

对于双曲型配极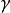 对应的二级曲线 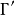，就一点与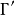 的关系而言，有以下三类：

1.切点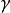： 的自共轭点称为 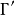的切点，切线就是过该点的自共轭直线，如图2中的点a；

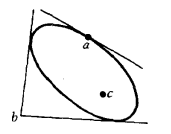
2.二切线点：有二自共轭直线通过的点称为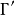 的二切线点，如图2中的点b；

3. 无切线点：无自共轭直线通过的点称为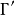 的无切线点，如图2中的点c2。

二级曲线的极点和极线配极变换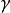 的极点和极线，称为其对应二级曲线的极点和极线。关于二级曲线的极点与极线有下面结果，

定理1对于二级曲线

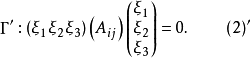
直线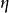 的极点方程为

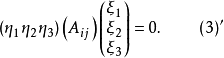
推论1 直线y关于二阶曲线(2)'的极点的坐标为

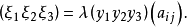
既然曲线的切线就是对应配极的自共轭直线，故它的极点是自共轭点，而自共轭点在曲线上，从而切线就是在曲线上的点的极线，该点就是切点，它是属于二级曲线的直线的极点。这样，我们立刻得到2

推论2 属于二级曲线(2)'的任意直线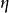 的切点方程为

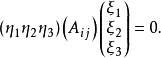
本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所