配极图形(polar figures)亦称共轭图形,是有特殊关系的两个图形,指在配极变换下成配极对应的两个图形。
基本概念给定二次曲线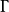 ,如果对平面上的每个点P,使P对应于点P关于
,如果对平面上的每个点P,使P对应于点P关于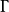 的极线
的极线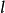 ,又对平面上的每条直线
,又对平面上的每条直线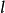 ,使
,使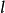 对应于直线
对应于直线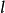 关于
关于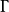 的极点,则在平面上的点与直线之间就建立了一个一一对应。这个对应称为关于
的极点,则在平面上的点与直线之间就建立了一个一一对应。这个对应称为关于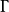 的配极或配极变换。在给定空间二次曲面
的配极或配极变换。在给定空间二次曲面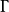 的情况下,同样可以通过使点对应于它的极面和使平面对应于它的极点来定义关于
的情况下,同样可以通过使点对应于它的极面和使平面对应于它的极点来定义关于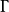 的配极或配极变换。配极变换是一种对偶变换。
的配极或配极变换。配极变换是一种对偶变换。
某个图形在关于一条二次曲线的配极变换下的象,称为原来图形的配极图形。给定的二次曲线在关于它本身的配极变换下的象,就成为二级曲线。二级曲线是二次曲线的配极图形。也可以类似地考虑关于二次曲面的配极图形1。
配极对应与配极图形在射影平而上,给定一非退化二阶曲线,其极点与极线构成了点与直线之间的一一对应关系。该同底点列与线束之间的对应称为配极对应,配极对应是一种异素对应,其代数表达式为 ,即
,即
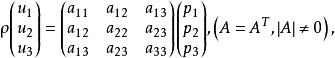 其中
其中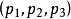 与
与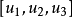 是对应极点与极线的坐标2。
是对应极点与极线的坐标2。
在配极对应下,射影平面上任一由点和直线构成的图形F对应于一由直线和点构成的图形F',F、F'称为一对相互配极的图形。当一个图形的配极图形与自身重合时称之为自配极的,自极三点形就是一个自配极的图形。
配极对应是非奇异的线性对应。于是,共线四点的交比与其四条对应极线(共点四线)的交比相等。
射影平面上一般的点线异素对应的代数表达式为 ,即
,即
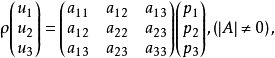 这里不要求A=AT,也是非奇异的线性对应2。
这里不要求A=AT,也是非奇异的线性对应2。
关于球的配极图形下面是极线最重要的性质。
定理 若点a在点b的极线上,那么反过来,点b也在点a的极线上3。
此时两点a和b称为对于圆的共轭点。它们的极线,就是说一条通过另外一条的极的两直线,也就称为共轭直线。
由于点a在点b的极线上(图1),那么它在Ob上的射影是一点K,满足Ok**·**Ob=R2,设H是b在Oa上的射影;四边形aHbK可内接于一圆周(以线段ab做直径的圆周),因而有
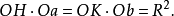
所以直线Hb是点a的极线。
备注:若直线ab与圆相交,定理是显然的。因为,此时假设和结论表达同一回事:圆周调和分割ab。
上面的定理,使我们可以从一个图形(F)的性质,得到另一个图形(F')的性质,我们立刻来定义这图形(F’),它称为(F)的配极图形或异素射(影)变(换)形3。
设(F)是由若干点和直线组成的图形(配极图形的定义也可以推广于含曲线的图形),此形的每一点a我们使它对应于一直线A,即点a对于某一圆的极线,这圆称之为导圆,一经选定便再也不变,图形(F)的每一直线B使之对应于一点b,即此直线对于导圆的极。直线A和点b组成一个图形(F’),即(F)的配极形。
由上面的定理得出以下的命题:
若图形(F)的直线B通过点a,那么图形(F')的对应点b在点a的对应线A上。
因此,若图形(F)的一直线绕一定点旋转,那么图形(F')的对应点描画一直线,反之亦然。
或者说,若图形(F)的三线共点,则图形(F')的对应三点共线,反之亦然3。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国