[科普中国]-对数似然方程

对数似然方程(log-likelihood equation)亦简称“似然方程”。对数似然方程与原似然方程同解，由于独立同分布的样本的似然函数上具有连乘积，对似然方程取对数更方便计算。

基本概念当总体X为连续型随机变量时，设其分布密度为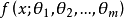，其中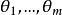为未知参数。又设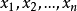为总体的一个样本，称

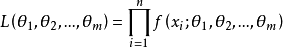为样本的似然函数，简记为。

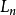当总体X为离散型随机变量时，设其分布律为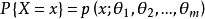，则称

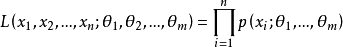为样本的似然函数****1。

若似然函数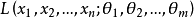在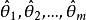处取到最大值，则称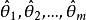分别为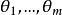的最大似然估计值，相应的统计量称为最大似然估计量。

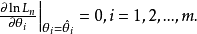
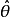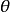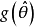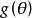若为的极大似然估计，g(x)为单调函数，则为的极大似然估计。

若似然函数为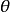的连续函数，且关于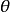的各分量的偏导数存在。设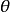是m维变量，且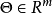为开区域，则由极值的一阶必要条件，得到

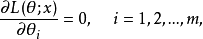通常称为似然方程，由于独立同分布的样本的似然函数上具有连乘积的形式，故对取对数后再求偏导数是方便的，因此实用上常采用与似然方程等价的形式1：

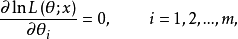称为对数似然方程。

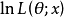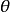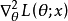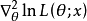值得注意的是：由极值的必要条件知，极大似然估计一定是似然方程或对数似然方程的解，但似然方程或对数似然方程的解未必都是极大似然估计，严格地讲，似然函数或对数似然函数对于参数的二阶Hesse矩阵或负定(若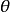是一元变量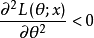，或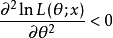)，则似然方程或对数似然方程的解才是极大似然估计1。

例题解析设总体X服从正态分布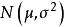，其中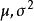为未知参数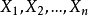，是来自总体X的一个样本，试用极大似然法估计参数。

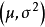正态分布的似然函数为2

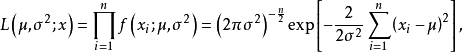相应的对数似然函数为

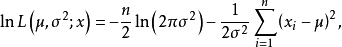令

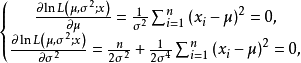解此似然方程组得到：

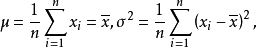进一步验证，对于对数似然函数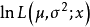的二阶Hesse矩阵

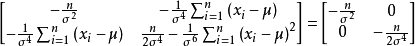是负定矩阵，故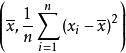是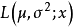的极大值。故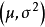的极大似然估计是1

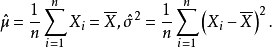
本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学