[科普中国]-网球拍定理

以网球拍为例可以出色地说明刚体具有不相等主惯性矩时其欧拉方程的解，称之为网球拍定理。1

判定内容网球拍的三个主轴易于判定如下：(1)沿把柄(2)垂直于把柄并在网的平面内(3)垂直于把柄和网，当使网球拍绕其主轴之一旋转的同时并把球拍抛入空中时，就会看到一种奇特的现象。如果初始旋转是绕着轴(1)或轴(3)，则拍子将继续绕初始轴均匀旋转，并且能很容易地再抓住。另一方面，如果起始是绕轴(2)旋转，则运动很快地变成不规则的，旋转演变成绕全部三个主轴进行，使得难以抓住下落的球拍，根据欧拉方程就可以解释所观察到的行状。为了把欧拉方程应用于网球拍，我们选择球拍的质心做为主轴坐标系的原点。

原理下面我们利用欧拉动力学方程来讨论欧拉不对称陀螺运动的稳定性问题。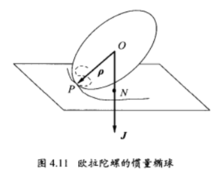

设陀螺的3个主转动惯量互不相等，不妨设，I1>I2>I3，惯量椭球为三轴椭球，如果陀螺绕3个主轴之一转动，则切点P与N点重合，空间极迹与本体极迹均退缩为一点，刚体的转轴保持不变，这是一种动平衡，转动的稳定性是指：如果转轴稍微偏离惯量主轴，这种偏离是否能够限制在一定的范围内，而不至越来越大?

(i)我们先看对于X3轴的微小偏离，这时在欧拉动力学方程中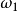 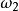， 为小量：

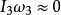
从而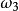 为常数。由欧拉方程可知，I3小于I1和I2，所以 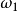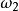， 不会越来越大，运动是稳定的。

(ii)再看转轴稍微偏离X1轴的情形，此时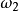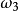，为小量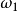，近似为常数，采用类似于(i)的步骤，可得：

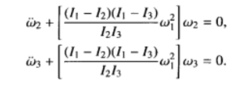
此时方括号内的常数大于零，故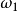 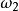，有振荡解，运动仍然是稳定的。

(iii)最后看转轴x2轴有微小偏离的情形，在这种情形中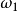 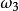，为小量，故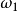 为常数，此时有：

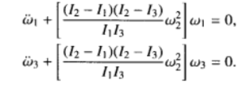
因I2小于I1，大于I3，方括号内常数小于零，方程的解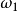 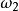，呈指数形式，故转动是不稳定的。

综上可得出结论：自由刚体绕主转动惯量最大或最小主轴的转动是稳定的，绕另一个主轴的转动不稳定，这一结论称为网球拍定理，这种效应很容易通过网球拍绕自身3个主轴的转动演示出来，这是因为在地球表面附近，重力是均匀分布的，所以球拍对于质心没有重力矩，如果略去风的阻力矩不计，则网球拍可视为一个欧拉不对称陀螺。2

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所