[科普中国]-奇异二次曲线

奇异二次曲线(singular quadratic curve)是二次曲线的特殊类型，若二次曲线是由两条直线构成的，则称为奇异的或退化的二次曲线。否则称为非奇异的或非退化的二次曲线1。

基本介绍若二次曲线是由两条直线构成的，则称为奇异的或退化的二次曲线，否则称为非奇异的或非退化的二次曲线。如果曲线方程为：

那么它是奇异二次曲线的充分必要条件是

二次曲线有奇点的充分必要条件为它是奇异的1。

相关介绍二次曲线与无穷远直线的相关位置

在仿射平面上，齐次仿射坐标满足三元二次方程

的点的集合叫做仿射平面上的二次曲线。在方程(1)中，系数aij为实数且至少有一个不为零，方程(1)叫做仿射平面上的二次曲线的方程2。

方程(1)可简写成

方程(1)也可以用矩阵表示为

其中矩阵叫做二次曲线(1)的系数矩阵，或表示系数行列式，且。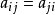

当时，则此二次曲线叫做非退化的二次曲线；当时，此二次曲线叫做退化的二次曲线。

现在求无穷远直线与二次曲线的交点，把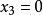代入方程(1)，得

从而解得

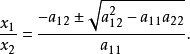
因此，当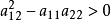时，方程(2)有两个不相等的实根；

当时，方程(2)有两个相等的实根；

当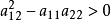时，方程(2)有两个共轭的虚根。

根据二次曲线与无穷远直线相交的情况，即根据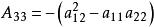的符号，我们把式(1)所表示的二次曲线进行分类2。

定义 当A33>0时，方程(1)所表示的曲线叫做椭圆型二次曲线；当A33=0时，方程(1)所表示的曲线叫做抛物型二次曲线；当A33