推理是利用显式储存的知识以产生另外显式知识的过程。推理过程也可分为两类,即演绎推理与非演绎推理。演绎推理,就是从一般性的前提出发,通过推导即演绎,得出具体陈述或个别结论的过程。非演绎推理是指结构化表示下的继承性推理,也是一种基本推理,数学证明中已存在但尚未认知的基本定理。由于知识处理的需要,提出了多种非演绎的推理方法,如连接机制推理、类比推理、基于示例的推理、反绎推理和受限推理等。
定义演绎推理是数学工作者经常要用的一种数学思维形式,演绎推理的作用在于从已知的知识得到未知的知识。非演绎推理是是已经存在但尚未认知的推理,非演绎推理的作用同样在于从已知的知识得到未知的知识。它的使用方法大致可分为三种:一是作为定理的全部证明,关于这一点下面还要提到;一是作为演绎推理的前提分析,这是最常见的一种;一是作为演绎推理的结论分析。非演绎推理是对薄莱尔预备定理证明中的演绎推理的结论进行分析。非演绎推理的使用方法,需要对反证法作点说明。
演绎推理与非演绎推理有共同之处也有不同之处。共同之处在于:第一,二者都是从前提推出结论;第二,非演绎推理除归纳法之外,与演绎推理一样,只要前提都真,则结论必真;第三,二者的作用相同,都是从已知的知识得到未知的知识;第四,二者都有一个前提分析过程。不同之处在于:第一,演绎推理从前提到结论之间的推理用的是逻辑推理;而非演绎推理的推理是根据具体问题具体分析进行的。由于非演绎推理与定理条件及证明方法等具体情况密切结合,因此在非演绎推理之中常常显示出推理的艰难、推理的技巧及推理的水平;第二,演绎推理的推理不涉及命题本身的内容,而非演绎推理的推理则不然;第三,演绎推理的前提与结论之间的关系必然为数理逻辑的逻辑演算中的形式定理所反映,而非演绎推理的相应关系则不能;第四,演绎推理对应着一个演绎推理规则,而非演绎推理则没有1。
类比推理类比推理是人类核心的认知能力之一,关注个体的认知发展,离不开对类比推理的探讨。类比推理简称类比,它是人类抽象逻辑的重要形式。从形式逻辑的角度讲,类比推理是指从两个(类)对象的相似性和一个(类)对象的已知特征推出另一个(类)对象也具有这个特征的过程。 研究中一般都采用上述定义,但要充分理解类比推理的内涵,与其实验任务是密不可分的。类比推理是哲学、逻辑学和心理学等学科研究的重要内容,是人类能够进行整合思维活动的重要机制,也是保证个体有效学习的工具。它的产生、发展和成熟是个体认知活动顺利完成的主要保障。类比推理的研究始终沿着两条路线前进:一条是研究类比推理的本质,另一条是研究类比推理与问题解决关系。尽管这些方面的研究获得了被学者们认同的结论,但在源类比物性质、过程限制及知觉特征对目标类比物的影响上,则存在不同主张。有代表性的理论如下:
结构映射理论(structure mapping theory)该理论是由Gentner.D(1983)提出来的,其基本思想是,类比中最关键因素是源类比物与目标类比物之间的联系。要实现这种联系,必须具备三个特征:一是结构连续性,即形成平行结构和一对一的对应关系。前者需要关系和主题的共同匹配,后者要求表征内的每个要素都要与另一表征内的要素形成匹配。二是以关系为中心性,即它要求类比物必须包括共同的关系而不是共同特征。三是系统性,即趋向于形成关系体系的匹配。例如,当一种结构上的联系给定后,就会从类比中产生进一步的推理,其含义是,系统性所蕴涵的意义在于产生自发性的推理。由此说来,结构映射理论对类比推理中关系的性质、特征要求很高,即对类比物的一致性、公平性和可匹配性要求更高。
多重限制理论,此理论的倡导者们(Keith Holyoak& Paul Thagard,1997)指出,类比的最后形成是由于在类比思维过程中大量结合在一起的总的限制所引起的:一是相似性限制,即类比在某种程度上是由于所含要素的直接相似所引起的;二是结构性限制,这种限制揭示的是类比映射和推理背后的关键的结构限制,就是在源类比物与目标类比物的各要素之间建立起连续的、一一对应的对应物的氛围;三是目标限制,要求推理者的目标与类比的目的(要解决什么问题)建立联系。从可被限制类比推理过程的因素来看,限制物越多,类比推理进行越困难。
高水平知觉理论,该理论(B.Markman,1997)指出,人的知觉分低、高两种水平。前者包括各种感觉中的信息加工过程;后者包括对低水平知觉加工的信息进行总体把握,并从这些精确的材料中提取意义,使之在概念水平上对情境进行知觉。这个范围包括从对事物的再认到抓住事物间抽象的联系,到对整个情境的理解和把握。即类比包括情境知觉过程和映射过程。在前个过程中,负责对材料过滤和组织,形成情境的心理表征。在后个过程中,同时激活两个情境表征,并形成一对一的对应,进而产生最后的类比。这两个过程是相互作用、不可分割的,即每个映射过程都需要知觉过程产生表征,而每一个知觉过程都需要映射过程的参与才能成为有意义的知觉。情境知觉水平越高,情境表征就越清晰,类比推理效果就越好2。
反绎推理溯因法或溯因推理(abductive reasoning,也译作反绎推理),是推理到最佳解释的过程。换句话说,它是开始于事实的集合,并推导出其最佳解释的推理过程。有时使用术语溯因(abduction)意味生成假设来解释观察或结论,但是前者定义在哲学和计算二者中更常见。
演绎:允许推导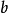 作为
作为 的结论,换句话说,演绎是推导已知事物的推论;
的结论,换句话说,演绎是推导已知事物的推论;
溯因:允许推导 作为
作为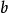 的解释,溯因同演绎反向,通过允许“
的解释,溯因同演绎反向,通过允许“ 蕴涵
蕴涵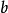 ”的前件
”的前件 推导自结论
推导自结论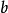 ;换句话说,溯因是解释已知事物的过程。在逻辑中,溯因法通过表示领域的逻辑理论
;换句话说,溯因是解释已知事物的过程。在逻辑中,溯因法通过表示领域的逻辑理论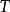 和观察的集合
和观察的集合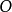 进行的。溯因是依据
进行的。溯因是依据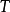 推导
推导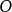 的解释的集合。
的解释的集合。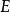 要成为
要成为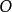 依据
依据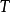 的解释,它应当满足两个条件:
的解释,它应当满足两个条件:
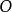 推导自
推导自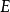 和
和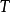 ;
;
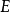 相容于
相容于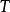 。
。
在形式逻辑中,假定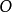 和
和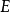 为文字的集合。
为文字的集合。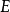 是
是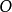 依据理论
依据理论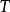 的解释的两个条件则形式化为:
的解释的两个条件则形式化为:
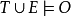 ;
;
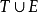 是相容的。
是相容的。
在满足这两个条件的可能的解释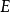 之中,通常施加一些其他的最小性条件来避免无关的事实(对
之中,通常施加一些其他的最小性条件来避免无关的事实(对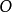 的蕴涵没有贡献)包含在解释中。
的蕴涵没有贡献)包含在解释中。
溯因法的一种不同的形式化是基于逆转计算假设的可见效果的函数。形式化的说,我们给出假设的集合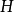 和表现(manifestation)的集合
和表现(manifestation)的集合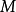 ;它们相关于领域知识,并以函数
;它们相关于领域知识,并以函数 所表示,这个函数接受假设的集合作为参数并给出对应的表现的集合作为结果。换句话说,对于假设的所有子集
所表示,这个函数接受假设的集合作为参数并给出对应的表现的集合作为结果。换句话说,对于假设的所有子集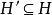 ,它们的效果通过
,它们的效果通过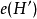 来知道。
来知道。
溯因法通过找到一个集合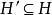 ,使得
,使得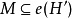 进行的。换句话说,溯因是通过找到假设的集合
进行的。换句话说,溯因是通过找到假设的集合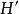 ,使得它们的效果
,使得它们的效果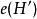 包含所有的观察
包含所有的观察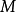 来进行的。
来进行的。
公共的假定是假设的效果是独立的,就是说,对于所有的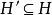 ,
,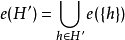 成立。如果这些条件满足,溯因法就可看作集合覆盖的一种形式。
成立。如果这些条件满足,溯因法就可看作集合覆盖的一种形式。
连接机制推理连接机制推理,更具体地说,就是以人工神经网络作为原型的知识表示方法。在人工智能研究中,这种知识表示方法可以说历经磨难。它的出现早于许多其它知识表示方法将近二十年,但在60年代末,由于寻找其有效学习算法的失败及对其泛化能力的怀疑,导致这种知识表示方法退出了人工智能的研究舞台,直到80年代初,人工智能研究者才将这类知识表示方法的原理以连接机制这个术语重新纳入人工智能研究的范围。当然使其在智能研究中占有一席之地的直接原因乃是 BP 算法的出现。尽管BP算法的成功是使其引起人工智能研究重新注意的原因,但这不是全部,更重要的是这种知识表示方法可以刻画那些使用局部表示难以描述的与感知类似的知识。例如,对于某些评价问题,领域的专家可以对他们熟悉的领域中的实例进行正确的评价,但是这些专家却难以解释对某个实例作出评价的理由,无论是统计意义下的理由,还是机理上的理由,而在多因素情况下甚至难以对这些因素进行排序,这就导致了使用局部表示的困难,即,大量的例外使系统难以承受,这就是知识的组合爆炸问题。从优化的角度来看,如果将实例理解为超平面上的一些点,原则上可以使用逼近理论来解决这个困难,但问题是什么样的数学基函数既可以给出在智能意义下的科学解释而又存在方便的数学处理方法呢。BP算法的贡献就是找到了符合这两个条件的数学基函数,而这个数学基函数就是连接机制的知识表示方法。对这类知识表示方法除了上述的优点之外, 并行性也是其重要的特性。但是,这种知识表示方法也同样存在显著的缺点,主要是学习收敛速度及泛化能力问题。前者无需多说,而后者则是由于这种表示所定义的数学空间与自然界中的问题空间之间存在巨大差异所造成的,而且这个差异将随问题规模的增加呈指数规律上升,其泛化能力则呈指数规律下降。从理论上还未找到有效的解决方法,而在技术上则采用与其它局部表示集成的方法来克服这个困难。基因表示与连接机制表示构成了知识表示体系树中的另一分支。
归纳推理归纳推理,又称基于示例的推理,是一种由个别到一般的推理。由一定程度的关于个别事物的观点过渡到范围较大的观点,由特殊具体的事例推导出一般原理、原则的解释方法。自然界和社会中的一般,都存在于个别、特殊之中,并通过个别而存在。一般都存在于具体的对象和现象之中,因此,只有通过认识个别,才能认识一般。人们在解释一个较大事物时,从个别、特殊的事物总结、概括出各种各样的带有一般性的原理或原则,然后才可能从这些原理、原则出发,再得出关于个别事物的结论。这种认识秩序贯穿于人们的解释活动中,不断从个别上升到一般,即从对个别事物的认识上升到对事物的一般规律性的认识。例如,根据各个地区、各个历史时期生产力不发展所导致的社会生活面貌落后,可以得出结论说,生产力发展是社会进步的动力,这正是从对于个别事物的研究得出一般性结论的推理过程,即归纳推理。显然,归纳推理是从认识研究个别事物到总结、概括一般性规律的推断过程。在进行归纳和概括的时候,解释者不单纯运用归纳推理,同时也运用演绎法。在人们的解释思维中,归纳和演绎是互相联系、互相补充、不可分割的。
本词条内容贡献者为:
王慧维 - 副研究员 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国