[科普中国]-辛标记

辛标记提供了一种既简单，又有效率的标记方法来展示方程及数学运算。辛标记的英文名 “Symplectic notation” 最先是德国著名数学家赫尔曼·外尔提出的。

定义在哈密顿力学里，因为哈密顿方程对于广义坐标q与广义动量p的运算在正负号上并不对称，必须用两个方程来表示：

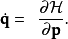
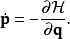这里，H是哈密顿量。

辛标记提供了一种既简单，又有效率的标记方法来展示方程及数学运算。辛标记的英文名 “Symplectic notation” 最先是德国著名数学家赫尔曼·外尔提出的。1 Symplectic 这字原来在希腊文是纠缠或编结的意思；用在这里主要是形容广义坐标和广义动量互相编结在一起的情况。

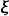设定一个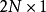的竖矩阵:

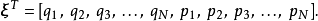此矩阵上半段是广义坐标、下半段是广义动量、T代表转置运算。我们也可以将 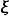视为一个向量。

定义辛矩阵为一个斜对称的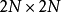方块矩阵：

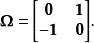这里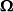，是由 4 个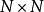零矩阵与单位矩阵组成。

这样，哈密顿方程可以简易的表示为

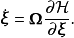
正则变换正则变换是一种正则坐标的改变，而同时维持哈密顿方程的形式，虽然哈密顿量可能会改变。所以，使用正则变换，正则坐标会从旧正则坐标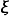 改变成新正则坐标 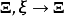；哈密顿量也从旧的哈密顿量H改变成新的哈密顿量 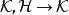；但是，哈密顿方程的形式仍旧维持不变：

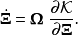
例子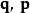在相空间中，用正则坐标，两个函数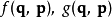的泊松括号记作:

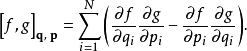
用辛标记，

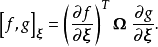
本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所