[科普中国]-复直线

复直线(complex line)是射影几何的基本概念之一，指以复数为坐标的直线，设直线的坐标为[u₁，u₂，u₃]，若u₁，u₂，u₃与三个不全为零的实数成比例，则称[u₁，u₂，u₃]为实直线。若u₁，u₂，u₃不与任何三个不全为零的实数成比例，则称[u₁，u₂，u₃]为虚直线。实直线与虚直线合称为复直线。在平面上引进复点以后，复直线便是坐标满足直线方程的复点的全体。例如，[1，0，2]与[i，0，2i]为同一条实直线，[i，1，1]是一条虚直线，(0，1，-1)与(i，1，0)都是这直线上的点1。

基本概念复点、复直线 以复数为坐标的点或直线称为复点或复直线。

复元素 复点和复直线统称复元素。

共轭复元素 若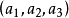 为一元素的齐次坐标时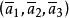， 为另一同类元素的齐次坐标，则此二元素叫做共轭复元素。

两个非无穷远共轭复元素，其非齐次坐标必为共轭复数。

两个共轭复元素的齐次坐标不一定为共轭复数，原因是齐次坐标可以相差一个常数因子2。

复点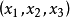 和复直线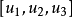 的结合关系为

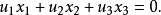
相关概念如果x,y这两个数都是复数，那么就称(x，y)为一个有穷远复点；如果x，y至少有一个是虚数，则称(x，y)为一个有穷远虚点；如果x，y都是实数，则称(x,y)为一个有穷远****实点。

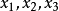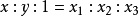可对有穷远复点(x，y)定义齐次坐标为：如果复数 满足 ，则称(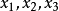 )为有穷远复点(x，y)的齐次坐标．此时 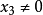。如果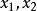 为复数，则称 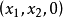为无穷远复点的齐次坐标。有穷远复点与无穷远复点统称为复点。所有复点的集合称为复射影平面。复点的齐次坐标不是唯一；同一复点的齐次坐标可以相差一个非零复因子；(0，0，0)不是任何复点的齐次坐标。

下面我们用i表示虚数单位。

一个虚齐次坐标有可能代表一个实点。例如(i，2i，-i)就代表实点(-1，-2)。一个复齐次坐标(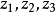 铂)代表实点的充分必要条件是它与实齐次坐标( 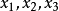)成比例。

满足齐次方程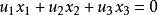 的复点(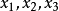 )的集合称为复直线，其系数[ 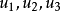]称为该复直线的齐次坐标。

设复点P的齐次坐标为(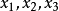 )，则称齐次坐标为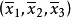的点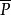为点P的共轭复点；设复直线l的齐次坐标为[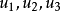]，则称齐次坐标为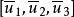]的复直线l为复直线l的共轭复直线。

我们把点I(1，i，0)和点J(1，-i，0)叫做圆点，过圆点I或J的直线叫做迷向直线。

共轭复点和共轭复直线统称为共轭复元素。注意，一对同类共轭复元素的齐次坐标不

必为共轭复数，因为同一点的齐次坐标可以相差一个非零复数。例如(2，i，1-i)与(2+2i，1-i，2i)是一对共轭复点的齐次坐标，这是因为

(2+2i，1-i，2i)=(1+i)(2，-i，1+i)=．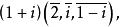

但显然(2，i，1-i)与(2+2i，1-i，2i)不是共轭复数3。

相关定理定理1 一元素为实元素的充要条件是该元素与其共轭复元素重合。

定理2 如果一点x在一直线u上，则共轭复点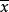必在共轭直线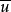上。

定理3 两共轭复直线的交点为一实点，两共轭复点的连线为一实直线。

推论 在一复直线上有唯一一个实点，过一复点有唯一一条实直线2。

注：一实直线上的点或为实点或为一共轭复点；过一实点的直线或为一实直线或为一共轭复直线。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所