近年来,协变经典场论又引起了研究者的兴趣。动力学在这里用有限维空间的在时空中的给定时间点上的场来表述。射流丛现在被认为是这种表述的正确定义域。 本文给出一阶经典场论的协变表述的一些几何结构。
记法本条目记法和射流丛条目所引入的一致。并令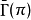 表示有紧支撑的
表示有紧支撑的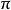 的截面。
的截面。
作用量积分一个经典场论数学上可以如下表述1:
1)一个纤维丛,其中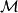 表示一个
表示一个 维时空。
维时空。
2)一个拉格朗日量形式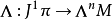
令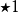 代表
代表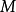 上的体积形式,则
上的体积形式,则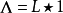 ,其中
,其中
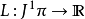
是拉格朗日量函数。 我们在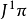 上选择纤维化坐标
上选择纤维化坐标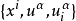 ,使得
,使得
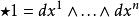
作用量积分定义为

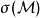 其中
其中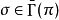 ,并定义于开集,而
,并定义于开集,而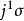 代表其第一射流延长(jet prolongation)。
代表其第一射流延长(jet prolongation)。
作用量积分的变分截面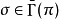 的变分由曲线
的变分由曲线 给出,其中
给出,其中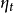 是一个
是一个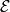 上的
上的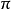 -竖直向量场
-竖直向量场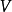 的流,它在
的流,它在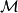 上有紧支撑。 截面
上有紧支撑。 截面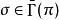 称为变分的驻点,如果
称为变分的驻点,如果
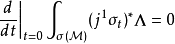
这等价于
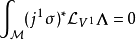
按导数的定义,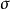 其中
其中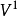 代表
代表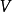 的第一延长。 使用嘉当公式
的第一延长。 使用嘉当公式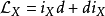 ,以及斯托克斯定理的支撑,可以证明这等价于
,以及斯托克斯定理的支撑,可以证明这等价于
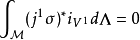
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国