[科普中国]-维德曼–夫兰兹定理

维德曼-夫兰兹定理是德国物理学家古斯塔夫·海因里希·维德曼（Gustav Heinrich Wiedemann）和鲁道夫·夫兰兹（Rudolph Franz）于1853年由大量实验事实发现，它描述了金属电导率σ和热导率ρ之间的关系。

详解维德曼-夫兰兹定理是德国物理学家古斯塔夫·海因里希·维德曼（Gustav Heinrich Wiedemann）和鲁道夫·夫兰兹（Rudolph Franz）于1853年由大量实验事实发现，它描述了金属电导率σ和热导率ρ之间的关系。1

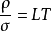
其中L称为洛伦茨系数，理论上，

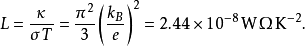
L和温度无关。为解释这个现象，考虑一个电子，它携带了一个负电荷，并处在外电场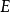中，那么它受到的力的大小为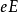。金属的电导率和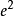成正比。而金属的热容和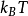成正比，电子受到了的力和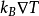成正比，因此金属的热导率和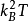成正比。综上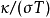，和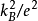成正比。使用玻尔兹曼方程可以证明以上表达式。

温度依赖值大于等于2.44×10W ^Ωķ的事实的结果在低温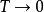（K）热和电荷电流由相同的准粒子携带：电子或空穴。在有限温度下，两种机制产生比率的偏差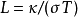。从理论Lorenz值L0:( i）以及其他热载流子，如声子或磁子来看，当温度趋于0K时，非弹性散射变弱并且促进大q散射值。对于每个传输的电子，还进行热激发并且Lorenz数达到L=L0。请注意，在完美的金属中，非弹性散射在极限中完全不存在 K和导热率会消失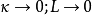。在有限温度下，小的q散射值是可能的，并且可以在不传输热激发L（T）L0。在德拜温度以上，声子对热传输的贡献是恒定的，并且再次发现比率L（T）是恒定的。

理论的局限性实验表明，对于所有材料，L的值虽然大致恒定，但并不完全相同。基特尔给出的一些值大号范围从大号=等于2.23×10W ^Ωķ 至大号等于 3.2×10W ^Ωķ 。Rosenberg指出，Wiedemann-Franz定律通常适用于高温和低温（即几开尔文）温度，但可能不适用于中等温度。

在许多高纯度金属中，电导率和导热率都随着温度的降低而升高。然而，在某些材料（例如银或铝）中，L的值也可能随温度而降低。在最纯净的银样品和非常低的温度下，L可以下降10倍。

在简并半导体中，Lorenz数L对某些系统参数具有很强的依赖性：维数，原子间相互作用强度和费米能级。这个定律是无效的，或者至少在以下情况下可以降低洛伦兹数的值：操纵电子态密度，改变超晶格中的掺杂密度和层厚度以及具有相关载流子的材料。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所