如果一个矢量场是某个标量势的梯度,那么便称为保守矢量场。有两个密切相关的概念:路径无关和无旋矢量场。任何一个保守矢量场的旋度都是零(因此是无旋的),也具有路径无关的性质。
定义一个矢量场 称为保守的1,如果存在一个标量场
称为保守的1,如果存在一个标量场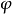 ,使得:
,使得:
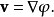
在这里,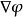 表示
表示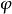 的梯度。当以上的等式成立时,
的梯度。当以上的等式成立时,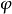 就称为
就称为 的一个标量势。
的一个标量势。
矢量分析基本定理表明,任何一个矢量场都可以表示为一个保守矢量场和一个螺线矢量场的和。
路径无关保守矢量场的一个重要性质是它沿着一条路径的积分只与起点和终点有关,与路径无关。假设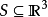 是三维空间内的一个区域,
是三维空间内的一个区域,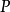 是
是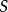 内的一个可求长路径,其起点为
内的一个可求长路径,其起点为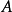 ,终点为
,终点为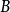 。如果
。如果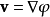 是保守矢量场,那么:
是保守矢量场,那么:
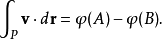
这是复合函数求导法则和微积分基本定理的结果。
一个等价的表述是,对于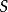 内的所有闭合路径,都有:
内的所有闭合路径,都有:
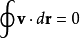
以上的逆命题也是成立的,只要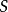 是连通区域。也就是说,如果
是连通区域。也就是说,如果 沿着
沿着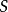 内的所有闭合路径的环量都是零,那么
内的所有闭合路径的环量都是零,那么 就是保守矢量场。
就是保守矢量场。
保守力如果力的矢量场是保守的,则这个力称为保守力。
最明显的例子是万有引力。根据牛顿万有引力定律,两个质点 和
和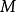 之间的引力
之间的引力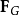 等于:
等于:
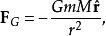
其中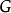 是引力常数,
是引力常数, 是单位矢量,从
是单位矢量,从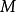 指向
指向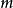 。万有引力是保守的,这是因为
。万有引力是保守的,这是因为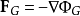 ,其中
,其中
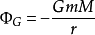
是引力势。
对于保守力,路径无关可以解释为从点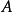 到点
到点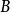 所做的功是与路径无关的,沿着闭合路径所做的功是零:
所做的功是与路径无关的,沿着闭合路径所做的功是零:
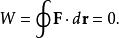
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国