热力学方格(英语:thermodynamic square),又称为热力轮(thermodynamic wheel)、古根海姆图(Guggenheim scheme)或玻恩方格(Born square),是由马克斯·玻恩提出的一种记忆术,用于快速建构热力学关系式。1929年,玻恩在课堂中提出热力学方格。F·O·柯尼希(Koenig)的论文中曾提及热力学的对称性。方格角落为共轭变数,而四边则是热动力位能。变数之间的放置和关系是记忆它们构成关系的关键。
使用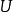 热力学方格主要用于计算任何感兴趣的热力学势的导数。1假设例如一个期望计算衍生物的的内部能量 。应考虑以下程序:
热力学方格主要用于计算任何感兴趣的热力学势的导数。1假设例如一个期望计算衍生物的的内部能量 。应考虑以下程序:
1)将自己置于感兴趣的热力学潜力中,即(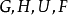 )。在我们的例子中,那就是
)。在我们的例子中,那就是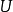 。
。
2)感兴趣的势头的两个相对角表示整体结果的系数。如果系数位于正方形的左侧,则应添加负号。在我们的例子中,中间结果将是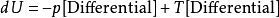 .
.
3)在每个系数的对角,您将找到相关的差分。在我们的例子中,对面的角落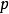 将会
将会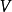 (卷)和对面的角落
(卷)和对面的角落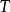 将会
将会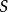 (熵)。在我们的示例中,中期结果将是:
(熵)。在我们的示例中,中期结果将是: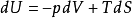 。请注意,符号约定仅影响系数而不影响差异。
。请注意,符号约定仅影响系数而不影响差异。
4)最后,总是添加 ,在哪里
,在哪里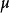 表示化学势。因此,我们会有:
表示化学势。因此,我们会有: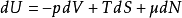 。
。
热力学平方也可用于找到麦克斯韦关系。望着广场的四个角落,制作一个 形状,人们可以找到
形状,人们可以找到
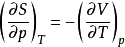 通过旋转
通过旋转 形状(随机,例如逆时针旋转90度成一个
形状(随机,例如逆时针旋转90度成一个 形状)其他关系如:
形状)其他关系如:
 可以被找寻到。
可以被找寻到。
最后,每一侧中心的电位是该侧角落处变量的自然函数。因此,G是p和T的自然函数,U是S和V的自然函数。
与麦克斯韦的关系1)要选择的是两个状态变量,它们位于正方形公共边的两个角上。
例如:找一个麦克斯韦关系与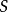 和
和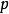 它形成了左边缘的角落。这些形成了所寻求的麦克斯韦关系的左侧的微分商,即
它形成了左边缘的角落。这些形成了所寻求的麦克斯韦关系的左侧的微分商,即
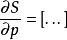 2)限制正方形相对侧的状态变量形成所寻求的麦克斯韦方程右侧的微分商。确保以与第一条边相同的方向读取它们。
2)限制正方形相对侧的状态变量形成所寻求的麦克斯韦方程右侧的微分商。确保以与第一条边相同的方向读取它们。
相反的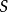 和
和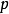 位于
位于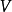 和
和 ,我们有
,我们有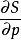 形成,所以“上角派生到下角”。因此,必须导出广场“从上到下”的另一侧。中期结果如下:
形成,所以“上角派生到下角”。因此,必须导出广场“从上到下”的另一侧。中期结果如下:
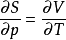 3)差异商,两者兼而有之
3)差异商,两者兼而有之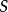 同样
同样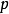 包含一个负号,因为两个(!)符号都在带有减号的边上。
包含一个负号,因为两个(!)符号都在带有减号的边上。
左侧收到负号。中间结果如下:
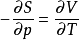 4)页面的常量保持变量总是在另一侧的分母中找到。
4)页面的常量保持变量总是在另一侧的分母中找到。
最终结果如下:
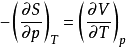
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国