[科普中国]-纠缠熵

一个由A部分和B部分组成的量子力学的系统，A与B之间可能存在某种远距离的相关性，即使A与B之间并不存在交互作用力，这种关联仍然存在，而且A部分和B部分的空间距离可以很远，这种概念称为纠缠。纠缠的强弱程度常利用纠缠熵来定量分析。事实上，纠缠的概念并不局限只把系统分成两个部分，但是多个部分的纠缠强弱在定量分析上遭遇许多困难，目前仍物理学家研究的课题之一。常见的纠缠熵都是定义在一个由A部分和B部分组成的纯态系统，例如：冯纽曼熵、仁义熵。

二分纠缠熵二元纠缠熵是关于将状态分成两个分区来定义的 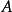和 。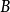

由纽曼纠缠熵二元冯诺依曼纠缠熵 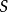被定义为其任一还原态的冯诺伊曼熵；结果与我们选择哪一个无关。也就是说，对于纯粹的状态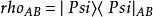

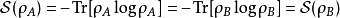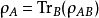哪里 和 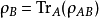是每个分区的简化密度矩阵。

当在纯态上评估时，许多纠缠措施降低到纠缠熵。

仁义纠缠熵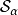也是根据降低密度矩阵和Renyi指数来定义的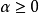。它被定义为降低密度矩阵的Rényi熵：

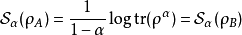请注意限制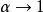，Renyi纠缠熵逼近冯诺依曼纠缠熵。

二部纠缠熵的面积法如果纠缠熵的前导项与两个分区之间的边界成比例增长，则量子态满足面积定律。1面积法则对于量子多体系统的基态是非常普遍的。这具有重要的应用，一个这样的应用是它大大降低了量子多体系统的复杂性。例如，密度矩阵重整化组和矩阵乘积状态隐含地依赖于这样的面积法则。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所