[科普中国]-二维共轭复元素

若(a1，a2，a3)为一个元素(点或直线)的齐次坐标，则由ai的共轭复数所成坐标构成的另一个同类元素为其共轭复元素，其主要结论有：1．一元素为实元素充分必要条件是该元素与其共轭复元素重合；2．若点x在直线u上，则x的共轭复点在u的共轭直线上；3．两共轭虚直线的交点为实点，两共轭虚点的连线为实直线；4．在一虚直线上有唯一实点，过一虚点有唯一一条实直线1。

基本介绍二维共轭复元素是复二维空间中坐标互相共轭的两个元素，若(a1，a2，a3)为一个元素(点或直线)的齐次坐标，取a1，a2，a3的共轭复数 ，则 为另一个同类元素(点或直线)的齐次坐标，此二元素称为二维共轭复元素(two-dimensionalconjugate complex elements)。因为齐次坐标允许差一个非零常数因子，所以两个第三坐标不是零的元素为共轭复元素时，必须且只须其对应的非齐次坐标为共轭复数，但两个共轭复元素的对应齐次坐标不一定为共轭复数。例如，(1-i，i，1)与(-1-i，i，-1)为两个共轭复点的齐次坐标，这是由于其非齐次坐标分别是(1-i，i)和(1+i，-i)2。

定理及推论定理1 一元素为实元素的充要条件为该元素与其共轭复元素重合。

定理2 如果点x在直线u上，则x的共轭复点 在u的共轭复直线u上。

定理****3 两共轭虚直线的交点为一实点，两共辐虚点的连线为一实直线。

推论 在一虚直线上有唯一一个实点，通过一虚点有唯一一条实直线3。

例题解析例1 证明：(2，i，1-i)与(2+2i，1-i，2i)表示一对共轭复点，并求其连线方程。

证： 点(2，i，1-i)之非齐次坐标为 ，

点(2+2i，1-i，2i)之非齐次坐标为 。

显然其坐标为共轭复数，所以此二点为共轭复点。其连线方程为：

即： 。

例2 (1)求过(1，i，0)之实直线；

(2)求直线[2，i，3-4i]上之实点。

解： (1)通过点(1，i，0)之实直线必过其共轭复点(1，-i，0)，故所求为 ；

(2)直线[2，i，3-4i]上之实点为它与共轭复直线[2，-i，3+4i]之交点，故所求为点(-3，8，2)。

例3 求无穷远直线 与圆 的交点。

解：解联立方程

得交点为和。

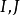注意 平面上一圆必经过两个共轭复点和，反之，一实二次曲线如果经过二点，则必为圆4。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所