[科普中国]-克莱罗定理

克莱罗定理于1743年由法国科学家克莱罗在其著作《关于地球形状的理论》（Théorie de la figure de la terre）中首次阐述。该定理给出了地球几何扁率与重力扁率的数学关系，为利用重力资料研究地球形状奠定了基础。

简介Clairaut theorem

克莱罗定理:

地球椭球扁率(α)和重力扁率(β)的近似关系式为：α+β=5q/2式中：q——地球赤道上的离心力与赤道上的正常重力之比。

内容克莱罗假设地球是由密度不同的均匀物质层圈组成的椭球体，各椭球面都是重力等位面，且各层密度由地心向外有规律的减小。椭球面上纬度为 φ 一点的重力加速度g 为：

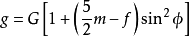
式中 G 为地球赤道上的重力加速度，m 为为赤道上的离心力与赤道上的重力加速度之比，f 为地球椭球扁率。1

历史尽管自古以来人们就已经知道地球是球形的，但到了17世纪，证据表明它并不是一个完美的球体。1672年，让·里奇发现了第一个证据表明重力在地球上不恒定（就像地球是一个球体一样）;他花了摆钟到卡宴，法属圭亚那，发现它失去了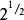相比，其在巴黎率每天分钟。这表明重力加速在卡宴比在巴黎少。摆重仪开始在世界的偏远地区航行，慢慢发现重力随着纬度的增加而平稳增加，两极的重力加速度比赤道大0.5%。

英国物理学家艾萨克·牛顿（Isaac Newton）在他的Principia Mathematica（1687）中解释了这一点，他在其中概述了他关于地球形状的理论和计算。牛顿正确地推理出地球不是一个球体，而是具有扁椭球形状，由于其旋转的离心力而在极点处略微变平。由于地球表面比赤道更靠近中心，所以重力更强。利用几何计算，他就地球的假想椭球体形状给出了具体的论点。

Principia的目标不是为自然现象提供确切的答案，而是为这些未解决的科学因素提供可能的解决方案。牛顿推动科学家进一步研究未解释的变量。他受到启发的两位杰出研究人员是Alexis Clairaut和Pierre Louis Maupertuis。他们都试图证明牛顿关于地球形状的理论的有效性。为了这样做，他们去拉普兰探险，试图精确测量子午线弧。从这些测量中，他们可以计算偏心率地球，它离开完美球体的程度。Clairaut证实，牛顿关于地球是椭圆形的理论是正确的，但他的计算是错误的，并且用他的发现给伦敦皇家学会写了一封信。该社团于1737年在哲学交易中发表了一篇文章，揭示了他的发现。Clairaut展示了牛顿方程是如何不正确的，并没有证明地球的椭球形状。然而，他纠正了理论的问题，实际上证明了牛顿的理论是正确的。Clairaut相信牛顿有选择他所做的形状的理由，但他在Principia中并不支持它。Clairaut的文章没有提供一个有效的等式来支持他的论点。这在科学界引起了很大争议。

直到1743年Clairaut写了Théoriede la figure de la terre，才提供了正确的答案。其中，他颁布了今天更为正式的Clairaut定理。

本词条内容贡献者为:

王宁 - 副教授 - 西南大学