[科普中国]-费歇耳信息矩阵

费歇耳信息矩阵是费歇耳信息量由单个参数到多个参数情形的推广。费歇耳信息量表示随机变量的一个样本所能提供的关于状态参数在某种意义下的平均信息量。费舍尔信息矩阵(FIM)是Fisher信息量的矢量化定义。

基本介绍一个样本观测值所能提供的关于未知多维参数θ=(θ1，θ2，…θm)的信息量期望值的一种度量——m×m矩阵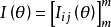 ，其中

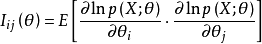
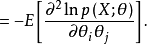式中p(x;θ)为总体X的概率函数。来自总体X的简单随机样本(X1，X2，…，Xn)所能提供的关于θ的费歇耳信息量为nI(θ)。这时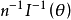， 是克拉默-拉奥方差界在多维情况下的类似：设 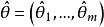是θ=(θ1，θ2，…，θm)的任一无偏估计量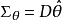， 是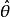 的方差矩阵，则 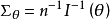是非负定矩阵1。

假设(X，Y)有二元正态分布，EX=EY =0，DX=DY =σ2，X和Y的相关系数为ρ，则参数θ=(σ2，ρ)的费歇耳信息矩阵为：

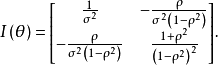
相关概念费歇耳信息量费歇耳信息量是一次观测值所能提供的关于未知参数θ的信息量期望值的一种度量，定义为

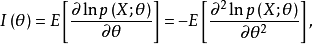其中p(x;θ)是总体的概率函数。

费歇耳信息量I(θ)具有如下性质：

1. 非负性：I(θ)≥0而I(θ)=0当且仅当p(x; θ)不依赖于θ；

2.可加性：n次独立重复观测值、即来自总体的简 单随机样本(X1，X2，…，Xn)所能提供的关于θ的信息量期望值为nI(θ)。

对于正态总体X～N(μ，σ)；I(μ)=1/σ2，I(σ2)=1/(2σ4)；对于参数为λ的泊松总体，I(λ)=1/λ。

克拉默-拉奥方差界克拉默-拉奥方差界是未知参数之一切可能估计量的方差的公共下界。2设总体X的概率函数p(x;θ)依赖于未知参数θ;g=g(θ)是参数θ的函数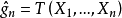， 是g的估计量，其中X1，…，Xn是来自X的简单随机样本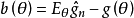； 是估计量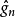 的偏倚，则

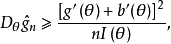其中I(θ)是θ的费歇耳信息量。此不等式称做“克拉默-拉奥(Cramer-Rao)不等式”，其右侧称做“克拉默-拉奥方差界”。 若 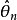是θ的无偏估计， 则有

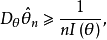
对于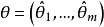 是多维参数的情形， 有类似的结果。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所