[科普中国]-量子势能

量子势能在1952年由戴维波姆（David Bohm12）首次提出，是德布罗意量子力学（物质波理论）的中心概念型式。1975年，Bohm和Basil Hiley3诠释其为作用在粒子上的信息势能。量子势能又可称为Bohm势能或量子Bohm势能。

在分子体系内部，化学键都有“自然”的键长值和键角值。分子要调整它的几何形状（构象），以使其键长值和键角值尽可能接近自然值，同时也使非键作用（van der Waals力）处于最小的状态，给出原子核位置的最佳排布。因此需要一个物理量来衡量体系内的原子分布是不是符合“自然状态”，这个物理量就是所谓的势能（Potential Energy4），因在哈密顿(Hamiltonian)表述中，势能习惯写为V，与电势V相同，因此也可由potential代指。

Bohm和Hiley对于量子势能的概念诠释导致物理学家开始注意到量子物理中最基本的新性质─非局域性(nonlocality)。

势能越高体系往往越不稳定，因为携带了更多可以转化的潜力。量子力学里的能量守恒是平均值守恒，能量平均值=动能平均值+势能平均值势能是分子体系中各种能量的总和，虽然相比于弹性势能和重力势能，分子体系的势能的组分更复杂，可以分成两大类：共价键势能和非共价相互作用能。

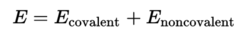
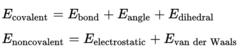势能只和原子间的相对坐标及原子带有的局部电荷相关。通过对势能函数的计算和优化，可以获得分子体系内各个原子之间处在什么样的相对坐标分布的情况下势能最低，这就是所谓的分子的低能构象或优势构象。

应用领域量子势能的方法可被用在量子效应的建模(modeling)上，不需明确地解出薛定谔方程。量子势能也可与蒙特卡洛(Monte Carlo method)模拟结合，模拟可用于(深)次微米元件的载子传输问题，如载子流体力学方程(Hydrodynamic, HD，此处指元件载子传输现象的动力方程，与流体无关，仅因描述公式的型式与传统流体力学相似而得名5)和扩散方程。此计算方法先决定各个流体元素(fluid element)的密度，接着流体元素的加速经由计算V和Q的梯度得出，最后速度场的散度决定密度的变化。在商用的元件模拟软件，如SILVACO TCAD，已可加入量子势能来模拟元件行为。

应用实例薛定谔方程中的量子势能。

薛定谔总方程式为：

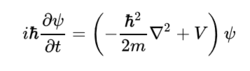可由含有实函数R和S的极坐标型式的波函数ψ改写。其中R和S分别为波函数的振幅和相位。改写后可将方程写成两个部分，分别对应到实部和虚部，实部部分称为量子哈密顿-亚克比方程(Hamilton-Jacobi equation)，虚部部分称为连续方程。

薛定谔方程虚部部分的连续方程

表达式：

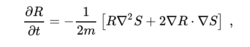如果ρ=R square，上式可变形为连续方程：

∂ρ/∂t+▽*（ρv) = 0

2. 薛定谔方程实部部分的量子哈密顿-亚克比方程

表达式：

量子哈密顿-亚克比方程与经典哈密顿-亚克比方程多出一项，如下所示：

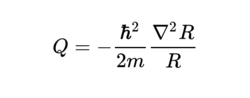其中，Q即为量子势能。该公式表示，量子势能与波函数振幅的曲率(curvature)有关。取极限为0时，函数h为经典哈密顿-亚可比方程的解，因此函数S又可称为哈密顿-亚可比函数，或者是可延伸至量子物理的作用量(action)。

总能，势能，动能之间的关系量子力学中，能量是总称动能，势能，机械能，热能等都是能量的一种。

能量包含动能和势能，动能+势能=机械能（外在能量）+热能（物体内在能量）=物体的能量

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所