绝对约束环境是指必须严格满足的等式或不等式约束的求解环境。如线性规划问题中的所有约束条件都是绝对约束,线性规划问题的求解环境就是绝对约束环境。
内容介绍绝对约束(硬约束)是指必须严格满足的等式或不等式约束,如线性规划问题中的所有约束条件都是绝对约束。
目标约束是目标规划特有的约束,它是把要追求的目标的理想值作为右端常数项,在目标表达式左端加减正负偏差变量构成的等式约束,目标约束是由决策变量、正负偏差变量及理想值构成的软约束。
在目标规划中,绝对目标约束就是必须要严格满足的约束。绝对目标约束是最高优先级,在考虑较低优先级的目标之前它们必须首先得到满足。1
比较线性规划只有一个目标函数,属于单目标问题。线性规划中,为得到一个可行解,必须满足所有的约束条件。线性规划中列出的约束条件均为严格满足的等式或不等式的约束,所以线性规划问题中的所有约束条件都是绝对约束,线性规划问题求解环境为绝对约束环境。
实际问题中往往要考虑多个目标,这一系列目标之间,不仅有主次之分,而且有时会互相矛盾。目标规划正是为了解决这类多目标问题而产生的一种方法。目标规划就是在满足现有的一组约束条件下,求出尽可能接近理想值的解,这个解称为满意解。在目标规划中,并不认为所有约束都是绝对的,因此对于非绝对的约束,目标规划并不要求绝对满足,而是设法使各目标离原先设定的意向指标值的偏差尽可能的小。所以目标规划问题求解环境不是绝对约束环境。2
转化绝对约束又称系统约束,是指必须严格满足的等式和不等式约束,如线性规划问题的所有约束都是绝对约束,不满足这些约束条件的解称为非可行解,所以它们是硬约束。对那些不严格限定的约束,连同原线性规划建模时的目标函数转化为的约束,均可通过目标约束来表达。绝对约束与目标约束的转化过程如下。1
将目标函数转化为目标约束:在引入了目标值和正、负偏差变量后,可以将原目标函数加上负偏差变量 ,减去正偏差变量,并令其等于目标值,这样形成一个新的函数方程,把它作为一个新的约束条件,加入到原问题中去,称这种新的约束条件为目标约束。
将绝对约束转化为目标约束:根据需要将绝对约束转化为目标约束,这时只须将该约束的右端项看作目标值,再引入正、负偏差变量即可。在达到此目标值时允许发生正或负偏差,因此在这些约束中加入正、负偏差变量,它们是软约束,在给定目标值和加入正、负偏差变量之后,可以将绝对约束转化为目标约束。
举例例1.工厂生产两种产品,受到原材料供应和设备工时的限制。在单件利润等有关数据已知的条件下,要求制订一个获利最大的生产计划,具体数据见下表1。
|| || 表1
解析:该问题属于线性规划问题,只有一个目标函数,约束条件均为严格满足的等式或不等式的约束,求解环境为绝对约束环境。因此设产品Ⅰ、Ⅱ的产量分别为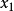 和
和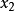 ,建立线性规划模型。
,建立线性规划模型。
目标函数: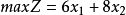 ;
;
约束条件: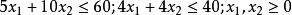 。
。
解得最优生产计划为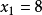 件,
件, 件,利润为
件,利润为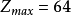 元。
元。
例2.接例1,如果工厂作决策时可能还需根据市场和工厂实际情况,考虑其它问题,如:
由于产品Ⅱ销售疲软,故希望产品Ⅱ的产量不超过产品Ⅰ的一半;
原材料严重短缺,原料数量只有60;
最好能节约4小时设备工时;
计划利润不少于48元。
解析:可知要求1,3,4为非绝对的约束,目标规划并不要求绝对满足,而是设法使各目标离原先设定的意向指标值的偏差尽可能的小,故求解环境为非绝对约束环境。
在例1中若工厂提出的管理目标按优先级排列如下: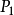 级目标:希望产品Ⅱ的产量不超过产品Ⅰ的一半;
级目标:希望产品Ⅱ的产量不超过产品Ⅰ的一半;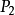 级目标:最好能节约4小时设备工时;
级目标:最好能节约4小时设备工时;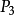 级目标:希望计划利润不小于48元;由于原材料严重短缺,故原材料约束作为绝对约束。建立目标规划模型。
级目标:希望计划利润不小于48元;由于原材料严重短缺,故原材料约束作为绝对约束。建立目标规划模型。
目标函数: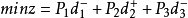 ;
;
约束条件: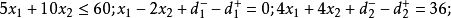
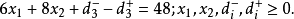
其中①为绝对约束,②、③、④为目标约束。3
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国