[科普中国]-冯纽曼熵

量子统计力学中，冯纽曼熵（英语：von Neumann entropy）是经典体系吉布士熵概念的拓展延伸。

数学表示体系的冯纽曼熵1为：

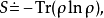其中 表示求迹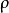， 是体系的密度矩阵。

运用密度矩阵的本征态向量分解表示

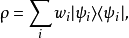可以得到：

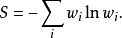
性质冯纽曼熵有下列性质：

1)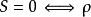 代表纯态；

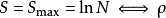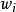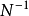2) 代表最大混合态，就是所有的 都等于 ，其中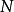 是希尔伯特空间的维数；

对密度矩阵作酉变换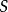， 不变。

3) 冯纽曼熵是密度矩阵的上凸函数：

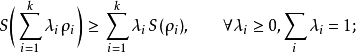4)冯纽曼熵对独立体系有加和性，就是：如果 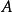和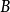 是两个独立的体系，这样

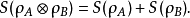
应用冯诺依曼熵在量子信息论框架下被广泛应用于不同的形式（条件熵，相对熵等）。纠缠度量基于与冯诺依曼熵直接相关的一些量。然而，在文献中已经出现了几篇关于香农信息量度可能不足的论文，并且因此冯诺依曼熵作为香农熵的适当量子推广。主要论据是，在经典测量中，香农信息测度是我们对系统性质的无知的一种自然度量，它的存在与测量无关。

相反，量子测量不能声称揭示在测量之前存在的系统的性质。这个争议促使一些作者引入Tsallis熵的非相加性质（标准Boltzmann-Gibbs熵的推广）作为在量子背景下恢复真实量子信息量度的主要原因，由于Tsallis熵的特殊性，应该描述局部相关性。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所