[科普中国]-随机游动模型

若时间序列{xt}适合于模型xt+xt-1=εt，其中{εt}是均值为零，方差为σε²的白噪声序列，则称其为随机游动模型。随机游动是一阶自回归模型[AR (1)]参数为a=1的极端情形。这时 {xt}不具有平稳性， 因为上述模型可以化为： xt=ε1+...+εs+...+εt，s=1,2,...,t，Var(xt)随t而增大，当t→∞时Var(xt)→∞，时间序列分析一般不对随机游动模型进行探讨研究1。

基本介绍对于AR(1)模型

它的平稳性条件是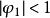。若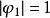，则不满足平稳性条件。(1)就成为

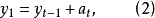称为随机游动模型。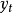表示游动者在t时刻的位置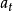，表示向前或向后的步幅。由(2)得到

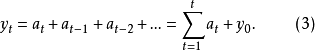显然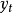，是随机过程，它是随机冲击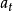在时间上的积累，其图形如图1所示。这说明历史上的任何一次冲击同目前的冲击起着同样的作用，而且不随时向的推移而消失。这里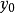是初始值。因此，这些冲击随时间的推移累积起来，其图像如图1那样随机地漂移，因而这一过程是非平稳的。其自相关函数为

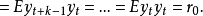
所以 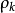=1，k=0，1，2，…

自相关函数的图像如图2所示。

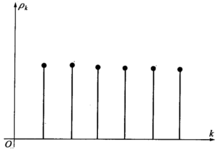
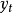的方差为

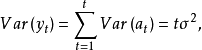由此可见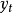的方差随t的增加而不断增大，因此，是一非平稳序列。

随机游动模型的经济原型，是由统计学家莫里斯·肯德尔(Maurice Kendall)在1953年发现的。其背景是英国皇家统计学会1953年在伦敦开会，讨论肯德尔写的一篇有争论的论文《经济时间序列分析》的第一部分：《价格》。肯德尔的初衷是想借助刚问世不久的电子计算机寻找股票价格波动的规律，但研究结果却有意外的发现，股市价格不但没有任何规律，而且就像一个醉汉走步一样，下周的价格等于本周的价格加上一个随机数字，也就是说股价近似遵从随机游动(RandomWalk)模型2。

随机游动模型的种类若(1)是下列形式

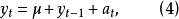式中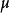为非零常数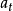，仍是随机冲击值，也就是白噪声序列，则称(4)为带漂移项的随机游动模型。通过对(4)的直接迭代，可得

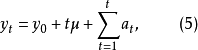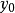这里是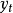的初始值。由此可见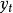的期望值为

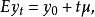方差为

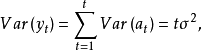方差随t的不断增加而不断增大，因此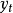是不平稳的随机序列。

若(5)是如下形式

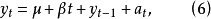
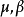均为常数，则称(6)为带线性趋势项的随机游动模型2。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所