拉普拉斯中心极限定理也称棣莫弗-拉普拉斯中心极限定理,它是关于二项分布渐近趋于正态分布的极限定理,因此,也称二项分布的中心极限定理,拉普拉斯中心极限定理是独立同分布中心极限定理(林德贝格-勒维中心极限定理)的特例。
大数定律只断言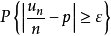 当
当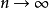 时趋于0,也即
时趋于0,也即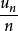 接近于
接近于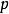 ,而拉普拉斯中心极限定理则给出
,而拉普拉斯中心极限定理则给出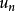 的渐近分布的更精确表述。
的渐近分布的更精确表述。
拉普拉斯中心极限定理给出了两个结果。第一个结果提供了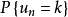 的渐近表达式,这类结果一般称为局部极限定理。第二个结果给出了标准化随机变量
的渐近表达式,这类结果一般称为局部极限定理。第二个结果给出了标准化随机变量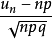 的渐近分布(其中
的渐近分布(其中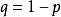 ),称为积分极限定理,它是独立同分布中心极限定理的特例。
),称为积分极限定理,它是独立同分布中心极限定理的特例。
定理若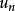 是n次伯努利试验中事件A出现的次数,
是n次伯努利试验中事件A出现的次数,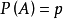 ,
,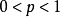 ,则对任意有限区间[a,b]:
,则对任意有限区间[a,b]:
(1)当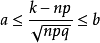 及
及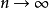 时,一致地有
时,一致地有
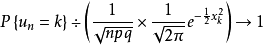 其中
其中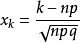 ,称为局部极限定理。
,称为局部极限定理。
(2)当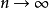 时,一致地有
时,一致地有
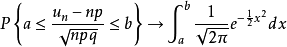 称为积分极限定理。1
称为积分极限定理。1
含义因为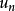 为n次伯努利试验中事件A发生的次数,故
为n次伯努利试验中事件A发生的次数,故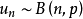 ,上述积分极限定理说明
,上述积分极限定理说明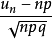 近似服从标准正态分布
近似服从标准正态分布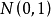 ,或者说,
,或者说,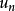 近似服从正态分布
近似服从正态分布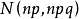 。
。
应用拉普拉斯中心极限定理虽然是作为二项分布的近似而推导出来的,但是它的重要性远远超出数值计算的范围。该定理的证明参见李贤平《概率论基础》289-292页1。
用频率估计概率时的计算问题由积分极限定理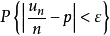 =
=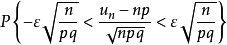
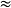
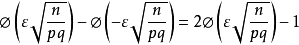 ,其中
,其中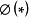 为标准正态分布的分布函数,显然,对任意的
为标准正态分布的分布函数,显然,对任意的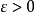 ,当
,当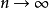 时有
时有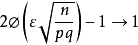 ,即
,即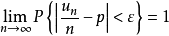 。
。
例:蒲丰试验中掷硬币4040次,出正面2048次,试计算当重复蒲丰试验时,正面出现的频率与概率之差的绝对值不大于蒲丰试验中所发生的偏离的概率。
解:蒲丰投币中频率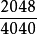 与概率
与概率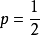 的偏离为
的偏离为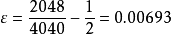 ,故所求概率为
,故所求概率为
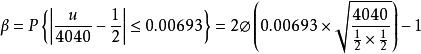
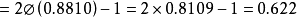
本词条内容贡献者为:
朱坤平 - 副教授 - 华东理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国