[科普中国]-逆狄利克雷分布

在统计学中，逆狄利克雷分布（Inverted Dirichlet distribution），又称**倒Dirichlet分布，**是贝塔分布的多变量泛化，并且与狄利克雷分布有关。它在1965年首次由Tiao和Cuttman描述。如果使用概率形式的比值比代替类别的概率，则逆狄利克雷分布与负多项分布共轭。

历史在统计学中，逆狄利克雷分布是贝塔分布的多变量泛化，并且与狄利克雷分布有关。它在1965年首次由Tiao和Cuttman描述。T. Bdiri等人已经开发了几种使用逆狄利克雷分布来表示和模拟非高斯数据的模型。他们引入了使用Newton-Raphson技术估计参数的逆狄利克雷分布的有限和无限混合模型，以及用于模拟无限混合的狄利克雷过程。T. Bdiri等人也使用逆狄利克雷分布来提出一种基于贝叶斯推断生成支持向量机内核方法，以及另一种建立层次聚类的方法。

定义逆狄利克雷分布具有由下式给出的密度函数：

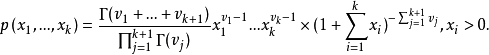该分布在统计回归中有应用，并在考虑多元学生分布时自然产生。它可以通过其时刻生成函数来表征：

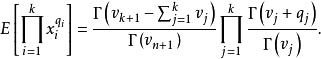
前提是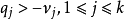 和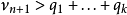 。如果使用概率形式的比值比代替类别的概率，则逆狄利克雷分布与负多项分布共轭。混合逆狄利克雷分布是正的非高斯数据分析中一个重要的统计模型1。

相关术语狄利克雷分布狄利克雷分布是一组连续多变量概率分布，是多变量普遍化的Β分布。为了纪念德国数学家约翰·彼得·古斯塔夫·勒热纳·狄利克雷（Peter Gustav Lejeune Dirichlet）而命名。狄利克雷分布常作为贝叶斯统计的先验概率。当狄利克雷分布维度趋向无限时，便成为狄利克雷过程（Dirichlet process）。狄利克雷分布奠定了狄利克雷过程的基础，被广泛应用于自然语言处理特别是主题模型（topic model）的研究2。

维度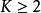 的狄利克雷分布在参数 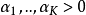上基于欧几里得空间 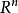里的勒贝格测度有个概率密度函数，定义为：

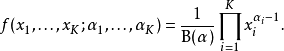
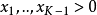并且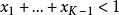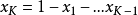，。在维的单纯形开集上密度为0。

归一化衡量B(α)是多项Β函数，可以用Γ函数（gamma function）表示：

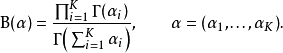
本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所